【题目】已知数列
满足
，
，其中
是等差数列，且
，则
________．
【答案】2018
【解析】
数列{an}、{bn}满足bn＝lnan，n∈N*，其中{bn}是等差数列，可得bn+1﹣bn＝lnan+1﹣lnan＝ln
常数t．常数et＝q＞0，因此数列{an}为等比数列．由
，
可得a1a1009＝a2a1008
．再利用对数运算性质即可得出．
解：数列{an}、{bn}满足bn＝lnan，n∈N*，其中{bn}是等差数列，
∴bn+1﹣bn＝lnan+1﹣lnan＝ln常数t．
∴常数et＝q＞0，
因此数列{an}为等比数列．
且，
∴a1a1009＝a2a1008．
则b1+b2+…+b1009＝ln（a1a2…a1009）
lne2018＝2018．
故答案为：2018．
科目：高中数学 来源： 题型：
【题目】下面有五个命题：
①函数
的最小正周期是
；
②终边在
轴上的角的集合是
；
③在同一坐标系中，函数
的图象和函数
的图象有三个公共点；
④把函数
的图象向右平移
个单位得到
的图象；
⑤函数
在
上是减函数；
其中真命题的序号是（ ）
A.①②⑤B.①④C.③⑤D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某游戏棋盘上标有第
、
、
、
、
站，棋子开始位于第站，选手抛掷均匀硬币进行游戏，若掷出正面，棋子向前跳出一站；若掷出反面，棋子向前跳出两站，直到跳到第
站或第站时，游戏结束.设游戏过程中棋子出现在第
站的概率为
.
（1）当游戏开始时，若抛掷均匀硬币
次后，求棋子所走站数之和
的分布列与数学期望；
（2）证明：
；
（3）若最终棋子落在第站，则记选手落败，若最终棋子落在第站，则记选手获胜.请分析这个游戏是否公平.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于函数的对称性有如下结论：对于给定的函数
，如果对于任意的
都有
成立
为常数），则函数
关于点
对称．
（1）用题设中的结论证明：函数
关于点
；
（2）若函数既关于点
对称，又关于点
对称，且当
时，
，求：①
的值；
②当
时，的表达式．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4－4：极坐标与参数方程
已知在平面直角坐标系xOy中，O为坐标原点，曲线C：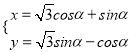 
(α为参数)，在以平面直角坐标系的原点为极点，x轴的正半轴为极轴，取相同单位长度的极坐标系，直线l：ρ
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程；
(Ⅱ)曲线C上恰好存在三个不同的点到直线l的距离相等，分别求出这三个点的极坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数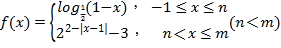
的值域是
，有下列结论：①当
时，
； ②当
时，
；③当
时，
； ④当时，
．其中结论正确的所有的序号是( )．
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
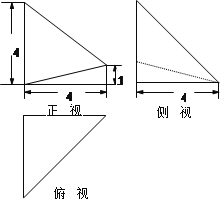
已知几何体A—BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
（1）求此几何体的体积V的大小；
（2）求异面直线DE与AB所成角的余弦值；
查看答案和解析>>
科目：高中数学 来源： 题型：
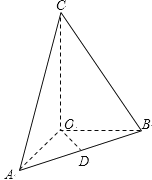
【题目】在三棱锥
中，OA、OB、OC所在直线两两垂直，且
，CA与平面AOB所成角为
，D是AB中点，三棱锥的体积是
．
（1）求三棱锥的高；
（2）在线段CA上取一点E，当E在什么位置时，异面直线BE与OD所成的角为
？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系上，有一点列
，设点
的坐标
（
），其中
． 记
，
，且满足
（
）．
（1）已知点
，点
满足
，求的坐标；
（2）已知点，
（），且
（）是递增数列，点
在直线
：
上，求
；
（3）若点
的坐标为
，
，求
的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com