

分析 设DF=m,CD=n,则由题意,tanθ=$\frac{n}{600+200\sqrt{3}+m}$,tan2θ=$\frac{n}{200\sqrt{3}+m}$,tan4θ=$\frac{n}{m}$,即可求出CD.
解答 解:设DF=m,CD=n,则由题意,
tanθ=$\frac{n}{600+200\sqrt{3}+m}$,tan2θ=$\frac{n}{200\sqrt{3}+m}$,tan4θ=$\frac{n}{m}$,
利用二倍角正切公式,代入计算解得θ=15°,m=100$\sqrt{3}$,n=300.
故答案为:300.
点评 本题考查二倍角的正切公式,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
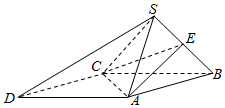 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,点E是SB的中点,∠SBC=45°,SC=SB=2$\sqrt{2}$,△ACD为等边三角形.
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,点E是SB的中点,∠SBC=45°,SC=SB=2$\sqrt{2}$,△ACD为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )
如图是某班50位学生期中考试化学成绩的频率分布直方图,其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则成绩在[70,90)内的频数为( )| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD中AB=2,BC=$\frac{{2\sqrt{3}}}{3}$,M,N分别为AB,CD中点,BD与MN交于O,现将矩形沿MN折起,使得二面角A-MN-B的大小为$\frac{π}{3}$,则折起后cos∠DOB为( )
如图,矩形ABCD中AB=2,BC=$\frac{{2\sqrt{3}}}{3}$,M,N分别为AB,CD中点,BD与MN交于O,现将矩形沿MN折起,使得二面角A-MN-B的大小为$\frac{π}{3}$,则折起后cos∠DOB为( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com