
【题目】如图,正方体![]() 的棱长为4,点E、F为棱CD、
的棱长为4,点E、F为棱CD、![]() 的中点.
的中点.
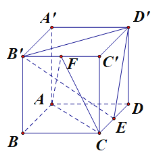
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面ACF所成角的正弦值.
与平面ACF所成角的正弦值.
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为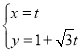 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阳马和鳖臑(bienao)是《九章算术·商功》里对两种锥体的称谓.如图所示,取一个长方体,按下图斜割一分为二,得两个模一样的三棱柱,称为堑堵(如图).再沿其中一个堑堵的一个顶点与相对的棱剖开,得四棱锥和三棱锥各一个,有一棱与底面垂直的四棱锥称为阳马(四棱锥![]() )余下三棱锥称为鳖臑(三棱锥
)余下三棱锥称为鳖臑(三棱锥![]() )若将某长方体沿上述切割方法得到一个阳马一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则可求出该阳马和鳖臑的表面积之和为( )
)若将某长方体沿上述切割方法得到一个阳马一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则可求出该阳马和鳖臑的表面积之和为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁餐厅新店开业,打算举办一次食品交易会,招待新老顾客试吃.项目经理通过查阅最近![]() 次食品交易会参会人数
次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数(万人) |
|
|
|
|
|
原材料(袋) |
|
|
|
|
|
(1)根据所给![]() 组数据,求出
组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,投入使用的每袋原材料相应的销售收入为
,投入使用的每袋原材料相应的销售收入为![]() 元,多余的原材料只能无偿返还,据悉本次交易大会大约有
元,多余的原材料只能无偿返还,据悉本次交易大会大约有![]() 万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式: ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项,共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,特招聘了3万名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
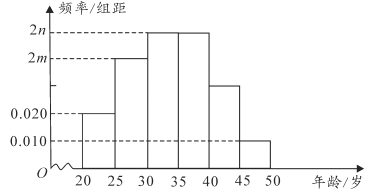
(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)本次军运会志愿者主要通过直接到武汉军运会执委会志愿者部现场报名和登录第七届世界军运会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: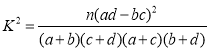 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有限个元素组成的集合![]() ,
,![]() ,记集合
,记集合![]() 中的元素个数为
中的元素个数为![]() ,即
,即![]() .定义
.定义![]() ,集合
,集合![]() 中的元素个数记为
中的元素个数记为![]() ,当
,当![]() 时,称集合
时,称集合![]() 具有性质
具有性质![]() .
.
(1)![]() ,
,![]() ,判断集合
,判断集合![]() ,
,![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)设集合![]() ,
,![]() 且
且![]() (
(![]() ),若集合
),若集合![]() 具有性质
具有性质![]() ,求
,求![]() 的最大值;
的最大值;
(3)设集合![]() ,其中数列
,其中数列![]() 为等比数列,
为等比数列,![]() (
(![]() )且公比为有理数,判断集合
)且公比为有理数,判断集合![]() 是否具有性质
是否具有性质![]() 并说明理由.
并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.
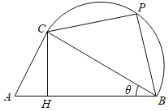
(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,a1=1,an>0,Sn2=an+12﹣λSn+1,其中λ为常数.
(1)证明:Sn+1=2Sn+λ;
(2)是否存在实数λ,使得数列{an}为等比数列,若存在,求出λ;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com