练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥P－ABCD中，底面ABCD为菱形，∠BAD＝60°，Q为AD的中点．

    (1)若PA＝PD，求证：平面PQB⊥平面PAD；

    (2)点M在线段PC上，PM＝tPC，试确定实数t的值，使得PA∥平面MQB.

    【答案】（1）详见解析（2）PM＝PC，t＝.

    【解析】试题分析：（1）要证平面平面，只要证平面，它可以由和得到．（2）中连接交于，交于，因为平面，故，由此可以得到，从而可以得到的大小．

    解析：(1)证明：连结，四边形为菱形，∵， ，∴为正三角形， 为的中点，∴.∵ ， 为的中点， ． 又，∴平面， 平面，∴平面平面．

    (2)当 时，使得平面，连接交于，交于，则为的中点．又∵为边的中线．∴为正三角形的中心. 令菱形的边长为a，则．∵平面， 平面，平面平面，∴， 即．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】（本题满分12分）已知椭圆C： 的离心率为， 是椭圆的两个焦点， 是椭圆上任意一点，且的周长是．

    （1）求椭圆C的方程；

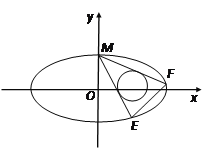
    （2）设圆T： ，过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点，当圆心在轴上移动且时，求EF的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)是定义在[－1,1]上的奇函数，在[0,1]上f(x)＝2x＋ln(x＋1)－1.

    (1)求函数f(x)的解析式；并判断f(x)在[－1,1]上的单调性(不要求证明)；

    (2)解不等式f(2x－1)＋f(1－x2)≥0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

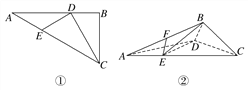
    【题目】如图①所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连接AB，BE，如图②所示，设点F是AB的中点．

    (1)求证：DE⊥平面BCD；

    (2)若EF∥平面BDG，其中G为AC上一点，求三棱锥B－DEG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （1）证明： ，直线都不是曲线的切线；

    （2）若，使成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个几何体的正视图和侧视图都是边长为1的正方形，且体积为，则这个几何体的俯视图可能是下列图形中的________．(填入所有可能的图形前的编号)

    ①锐角三角形；②直角三角形；③钝角三角形；④四边形；⑤扇形；⑥圆．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， （为自然对数的底数）．

    （Ⅰ）当时，求函数在点处的切线方程；

    （Ⅱ）若函数有两个零点，试求的取值范围；

    （Ⅲ）当时， 恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本．用系统抽样法，将全体职工随机按1～200编号，并按编号顺序平均分为40组(1～5号，6～10号，…，196～200号)．若第5组抽出的号码为22，则第8组抽出的号码应是________．若用分层抽样法，则40岁的以下的年龄段应抽取__________人．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为（为参数），将曲线上各点的横坐标都缩短为原来的倍，纵坐标坐标都伸长为原来的倍，得到曲线，在极坐标系（与直角坐标系取相同的单位长度，且以原点为极点，以轴非负半轴为极轴）中，直线的极坐标方程为．

    （1）求直线和曲线的直角坐标方程；

    （2）设点是曲线上的一个动点，求它到直线的距离的最大值．

    查看答案和解析>>

    同步练习册答案