
【题目】某区在2019年教师招聘考试中,参加![]() 、
、![]() 、
、![]() 、
、![]() 四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)从表中所有应聘人员中随机抽取1人,试估计此人被录用的概率;
(2)将应聘![]() 岗位的男性教师记为
岗位的男性教师记为![]() ,女性教师记为
,女性教师记为![]() ,现从应聘
,现从应聘![]() 岗位的6人中随机抽取2人.
岗位的6人中随机抽取2人.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人性别不同”,求事件
为事件“抽取的2人性别不同”,求事件![]() 发生的概率.
发生的概率.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(ii)
;(ii)![]() .
.
【解析】
(1)根据表中的数据,得到表中所有应聘人数为![]() ,被录用的人数为
,被录用的人数为![]() ,利用古典概型及概率的计算公式,即可求解;
,利用古典概型及概率的计算公式,即可求解;
(2)(i)记应聘![]() 岗位的男性为
岗位的男性为![]() ,
,![]() ,
,![]() ,应聘
,应聘![]() 岗位的女性为
岗位的女性为![]() ,
,![]() ,
,![]() ,利用列举法,即可求解;(ii)列举出事件
,利用列举法,即可求解;(ii)列举出事件![]() “抽取的2人性别不同”所含基本事件的个数,利用古典概型及概率的计算公式,即可求解.
“抽取的2人性别不同”所含基本事件的个数,利用古典概型及概率的计算公式,即可求解.
(1)因为表中所有应聘人数为![]() ,被录用的人数为
,被录用的人数为![]() .
.
所以从表中所有应聘人员中随机选择1人,此人被录用的概率约为![]() .
.
(2)(i)记应聘![]() 岗位的男性为
岗位的男性为![]() ,
,![]() ,
,![]() ,应聘
,应聘![]() 岗位的女性为
岗位的女性为![]() ,
,![]() ,
,![]() ,
,
从应聘![]() 岗位的6人中随机选择2人,共有15种结果,分别为:
岗位的6人中随机选择2人,共有15种结果,分别为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(ii)事件![]() “抽取的2人性别不同”情况有9种:
“抽取的2人性别不同”情况有9种:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
∴事件![]() 发生的概率为
发生的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若![]() ,对于给定实数
,对于给定实数![]() ,总存在实数
,总存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 恰有3个不同的实数根.
恰有3个不同的实数根.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)记![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的极坐标方程为
的极坐标方程为![]() (常数
(常数![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为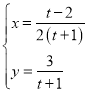 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和
的直角坐标方程和![]() 的普通方程;
的普通方程;
(2)若曲线![]() ,
,![]() 有两个不同的公共点,求实数
有两个不同的公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为A,过
,上顶点为A,过![]() 的直线
的直线![]() 与y轴交于点M,满足
与y轴交于点M,满足![]() (O为坐标原点),且直线l与直线
(O为坐标原点),且直线l与直线![]() 之间的距离为
之间的距离为![]() .
.
(1)求椭圆C的方程;
(2)在直线![]() 上是否存在点P,满足
上是否存在点P,满足![]() ?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点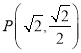 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .
.
(i)证明:直线![]() 与坐标轴平行;
与坐标轴平行;
(ii)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角P﹣AB﹣C的大小为120°,且∠PAB=∠ABC=90°,AB=AP,AB+BC=6.若点P,A,B,C都在同一个球面上,则该球的表面积的最小值为( )
A.45πB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 过焦点
过焦点![]() 且与抛物线交于
且与抛物线交于![]() 、
、![]() 两点,当直线
两点,当直线![]() 的倾斜角为30°时,
的倾斜角为30°时,![]() .
.
(1)求抛物线方程.
(2)在平面直角坐标系![]() 中,是否存在定点
中,是否存在定点![]() ,当直线
,当直线![]() 绕
绕![]() 旋转时始终都满足
旋转时始终都满足![]() 平分
平分![]() .若存在,求出
.若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com