
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |

分析 (Ⅰ)由已知作出频率分布表,由此能作出作出这些数据的频率分布直方图.
(II)由频率分布直方图能求出质量指标值的样本平均数、中位数位.
(Ⅲ)质量指标值不低于95的产品所占比例的估计值.由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品80%的规定.
解答 解:(Ⅰ)由已知作出频率分布表为:
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
| 频率 | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
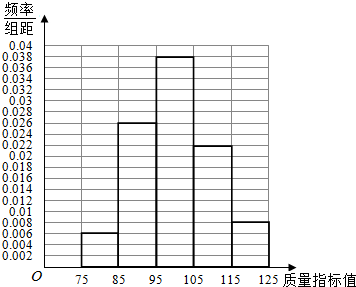
点评 本题考查频率分布直方图的作法,考查平均数、众数、中位数、方差的求法,考查产品质量指标所占比重的估计值的计算与应用,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{11π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
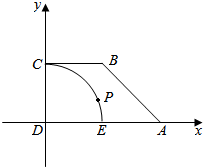 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com