
分析 由题意和三角形的面积公式列出方程,化简后得到a、b、c的关系,由余弦定理求出cosA的值.
解答 解:∵△ABC三边a,b,c上的高分别为$\frac{1}{2},\frac{{\sqrt{2}}}{2},1$,
∴$\frac{1}{2}×\frac{1}{2}×a=\frac{1}{2}×\frac{\sqrt{2}}{2}×b=\frac{1}{2}×1×c$,
则$a=\sqrt{2}b=2c$,即c=$\frac{1}{2}$a,b=$\frac{\sqrt{2}}{2}$a,
由余弦定理得,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$
=$\frac{\frac{1}{2}{a}^{2}+\frac{1}{4}{a}^{2}-{a}^{2}}{2×\frac{\sqrt{2}}{2}a×\frac{1}{2}a}$=$-\frac{{\sqrt{2}}}{4}$,
故答案为:$-\frac{{\sqrt{2}}}{4}$.
点评 本题考查余弦定理,以及三角形的面积公式的应用,考查化简、变形能力.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$是偶函数 | B. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$是奇函数 | ||
| C. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$不是奇函数 | D. | ?m∈R,函数f(x)=m+$\frac{1}{{{2^x}+1}}$不是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直.
如图,等腰梯形ABCD中,AB∥CD,AD⊥BD,矩形ABEF所在的平面和平面ABCD相互垂直. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
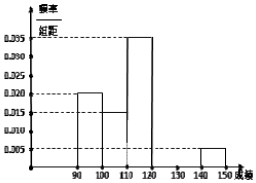 某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试结束后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分为六组,第一组.如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
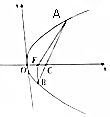 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在x轴上,记△BCF的面积为S1,△ACF的面积为S2,则$\frac{{S}_{1}^{2}}{{S}_{2}^{2}}$等于是( )| A. | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B. | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C. | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D. | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{63}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{63}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com