
分析 (1)根据题意,建立函数关系,可得分段函数模型;
(2)求出平均每件纪念品的利润函数,利用基本不等式求最值.
解答 解:(1)当150<x≤200(x∈N*)时,u(x)=150-(x-150)=300-x,
此时u(200)=100;
当200<x≤250(x∈N*)时,u(x)=u(200)-1.2(x-200)=-1.2x+340,
则u(x)=$\left\{\begin{array}{l}{300-x,150<x≤200}\\{-1.2x+340,200<x≤250}\end{array}\right.$,其中x∈N*;
(2)当150<x≤200(x∈N*)时,u(x)=300-x,
∴y=x-20-$\frac{14400}{u(x)}$=x-20-$\frac{14400}{300-x}$=-[(300-x)+$\frac{14400}{300-x}$]+280,
∵300-x>0,∴(300-x)+$\frac{14400}{300-x}$≥240,
当且仅当300-x=$\frac{14400}{300-x}$,即x=180时,等号成立,
∴y≤40,当且仅当x=180时,等号成立,即当x=180时,平均每件纪念品的利润y最大.
点评 本题考查函数的应用问题,根据条件建立函数关系,利用基本不等式求最值,确定函数模型是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
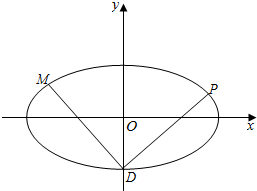 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(a)}{a}$>$\frac{f(b)}{b}$>$\frac{f(c)}{c}$ | B. | $\frac{f(c)}{c}$>$\frac{f(b)}{b}$>$\frac{f(a)}{a}$ | C. | $\frac{f(b)}{b}$>$\frac{f(a)}{a}$>$\frac{f(c)}{c}$ | D. | $\frac{f(a)}{a}$>$\frac{f(c)}{c}$>$\frac{f(b)}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com