
【题目】设椭圆![]() :
:![]() (
(![]() ),左、右焦点分别是
),左、右焦点分别是![]() 、
、![]() 且
且![]() ,以
,以![]() 为圆心,3为半径的圆与以
为圆心,3为半径的圆与以![]() 为圆心,1为半径的圆相交于椭圆
为圆心,1为半径的圆相交于椭圆![]() 上的点
上的点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() :
:![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,过点
上任意一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,射线
两点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]()
①求![]() 的值;
的值;
②令![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)运用圆与圆的位置关系,![]() 和
和![]() 的关系,计算即可得到
的关系,计算即可得到![]() ,进而得到椭圆
,进而得到椭圆![]() 的方程;
的方程;
(2)求得椭圆![]() 的方程,①设
的方程,①设![]() ,
,![]() ,求得
,求得![]() 的坐标,分别代入椭圆
的坐标,分别代入椭圆![]() 的方程,化简整理,即可得到所求值;
的方程,化简整理,即可得到所求值;
②设![]() ,
,![]() 将直线
将直线![]() 代入椭圆
代入椭圆![]() 的方程,运用韦达定理,三角形的面积公式,将直线
的方程,运用韦达定理,三角形的面积公式,将直线![]() 代入椭圆
代入椭圆![]() 的方程,由判别式大于0,可得
的方程,由判别式大于0,可得![]() 的范围,结合二次函数的最值,,
的范围,结合二次函数的最值,,![]() 的面积为
的面积为![]() ,即可得到所求的最大值.
,即可得到所求的最大值.
解:(1)由题意可知,![]() ,可得
,可得![]() ,
,
又![]()
![]() ,
,
![]() ,
,
![]()
即有椭圆![]() 的方程为
的方程为![]() ;
;
(2)由(1)知椭圆![]() 的方程为
的方程为![]() ,
,
①设![]() ,
,![]() ,由题意可知,
,由题意可知,
![]() ,由于
,由于![]() ,
,
代入化简可得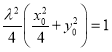 ,
,
所以![]() ,即
,即![]() ;
;
②设![]() ,
,![]() ,将直线
,将直线![]() 代入椭圆
代入椭圆![]() 的方程,可得
的方程,可得
![]()
![]() ,由
,由![]() ,可得
,可得![]() ,③
,③
则有![]() ,
,![]() ,
,
所以![]() ,
,
由直线![]() 与
与![]() 轴交于
轴交于![]() ,
,
则![]() 的面积为
的面积为![]()
![]()
设![]() ,则
,则![]() ,
,
将直线![]() 代入椭圆
代入椭圆![]() 的方程,
的方程,
可得![]()
![]() ,
,
由![]() 可得
可得![]() ,④
,④
由③④可得![]() ,则
,则![]() 在
在![]() 递增,即有
递增,即有![]() 取得最大值,
取得最大值,
即有![]() ,即
,即![]() ,取得最大值
,取得最大值![]() ,
,
由①知,![]() 的面积为
的面积为![]() ,
,
即![]() 面积的最大值为
面积的最大值为![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】某校高二理科1班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
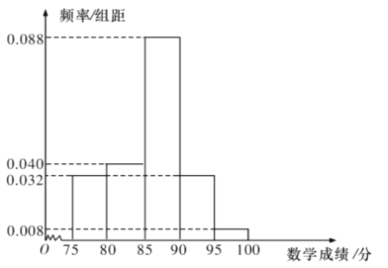
(1)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(2)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有X人,求X的分布列和数学期望;
(3)根据(1)(2)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
语文优秀 | 语文不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 |
附:①若![]() ,则
,则![]() ,
,![]() ;②
;②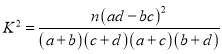 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设国家收购某种农产品的价格是1.2元/kg,其中征税标准为每100元征8元(即税率为8个百分点,8%),计划可收购![]() kg.为了减轻农民负担,决定税率降低
kg.为了减轻农民负担,决定税率降低![]() 个百分点,预计收购可增加
个百分点,预计收购可增加![]() 个百分点.
个百分点.
(1)写出税收![]() (元)与
(元)与![]() 的函数关系;
的函数关系;
(2)要使此项税收在税率调节后不低于原计划的78%,确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() 将函数
将函数![]() 图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移
图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)当![]() ,求实数
,求实数![]() 与正整数
与正整数![]() ,使
,使![]() 在
在![]() 恰有2019个零点.
恰有2019个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
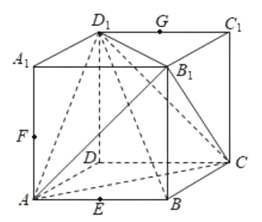
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,
,![]() ,对于定义在
,对于定义在![]() 上的函数
上的函数![]() ,有下述命题:
,有下述命题:
①“![]() 是奇函数”的充要条件是“函数
是奇函数”的充要条件是“函数![]() 的图像关于点
的图像关于点![]() 对称”;
对称”;
②“![]() 是偶函数”的充要条件是“函数
是偶函数”的充要条件是“函数![]() 的图像关于直线
的图像关于直线![]() 对称”;
对称”;
③“![]() 是
是![]() 的一个周期”的充要条件是“对任意的
的一个周期”的充要条件是“对任意的![]() ,都有
,都有![]() ”;
”;
④“函数![]() 与
与![]() 的图像关于
的图像关于![]() 轴对称”的充要条件是“
轴对称”的充要条件是“![]() ”
”
其中正确命题的序号是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新冠肺炎疫情的影响下,南充高中响应“停课不停教,停课不停学”的号召进行线上教学,高二年级的甲乙两个班中,需根据某次数学测试成绩选出某班的5名学生参加数学竞赛决赛,已知这次测试他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
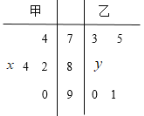
(1)求出x,y的值,且分别求甲乙两个班中5名学生成绩的方差![]() ,并根据结
,并根据结
果,你认为应该选派哪一个班的学生参加决赛?
(2)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com