
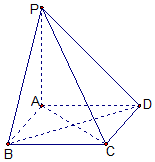
 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.求二面角P-CD-B余弦值的大小.  期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD的中点,PA⊥AD,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD的中点,PA⊥AD,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间(-1,0)内没有实数根 | |
| B. | 在区间(-1,0)内有一个实数根,在(-1,0)外有一个实数根 | |
| C. | 在区间(-1,0)内有两个相等的实数根 | |
| D. | 在区间(-1,0)内有两个不相等的实数根 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年陕西省高一下学期期末考数学试卷(解析版) 题型:选择题
为了得到函数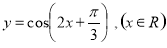 的图像,只需把函数
的图像,只需把函数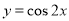 的图像
的图像
A.向左平行移动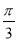 个单位
个单位
B.向右平行移动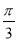 个单位
个单位
C.向左平行移动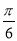 个单位
个单位
D.向右平行移动个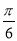 单位
单位
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 66 | C. | 72 | D. | 78 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com