
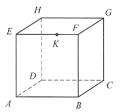
【题目】如图,正方体ABCD-EFGH的一个截面经过顶点A、C及棱EF上一点K,且将正方体分成体积比为3:1的两部分,则![]() 的值为______ .
的值为______ .
【答案】![]()
【解析】
记![]() 为截面所在平面,延长AK、BF交于点P,则P在
为截面所在平面,延长AK、BF交于点P,则P在![]() 上,故直线CP是
上,故直线CP是![]() 与平面BCGF的交线,设CP与FG交于点L,则四边形AKLC为截面,且ABC-KFL为棱台,不妨设正方体棱长为1,则正方体体积为1,设PF=h,则
与平面BCGF的交线,设CP与FG交于点L,则四边形AKLC为截面,且ABC-KFL为棱台,不妨设正方体棱长为1,则正方体体积为1,设PF=h,则![]() ,由条件知棱台ABC-KFL的体积
,由条件知棱台ABC-KFL的体积![]() ,列出方程可得h的值,可得答案.
,列出方程可得h的值,可得答案.
解:如图,记![]() 为截面所在平面.延长AK、BF交于点P,则P在
为截面所在平面.延长AK、BF交于点P,则P在![]() 上,故直线CP是
上,故直线CP是![]() 与平面BCGF的交线.设CP与FG交于点L,则四边形AKLC为截面.
与平面BCGF的交线.设CP与FG交于点L,则四边形AKLC为截面.

因平面ABC平行于平面KFL,且AK、BF、CL共点P,故ABC-KFL为棱台.不妨设正方体棱长为1,则正方体体积为1,结合条件知棱台ABC-KFL的体积![]() .
.
设PF=h,则![]() .
.
注意到PB、PF分别是棱锥P-ABC与棱锥P-KFL的高,于是
![]()
![]()
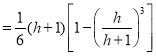
![]() .
.
化简得3h2=1,故![]() .
.
从而![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
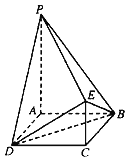
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年郑开国际马拉松比赛,于2019年3月31日在郑州、开封举行.某学校本着“我运动,我快乐,我锻炼,我提高”精神,积极组织学生参加比赛及相关活动,为了了解学生的参与情况,从全校学生中随机抽取了150名学生,对是否参与的情况进行了问卷调查,统计数据如下:
会参与 | 不会参与 | |
男生 | 60 | 40 |
女生 | 20 | 30 |
(1)根据上表说明,能否有97.5%的把握认为参与马拉松赛事与性别有关?
(2)现从参与问卷调查且参与赛事的学生中,采用按性别分层抽样的方法选取8人参加2019年马拉松比赛志愿者宣传活动,
①求男、女学生各选取多少人;
②若从这8人中随机选取2人到校广播站开展2019年赛事宣传介绍,求恰好选到2名男生的概率.
附:参考公式:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C的渐近线方程为![]() ,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动圆![]() 与圆
与圆![]() 外切,并与直线
外切,并与直线![]() 相切,则动圆圆心
相切,则动圆圆心![]() 的轨迹方程为__________,过点
的轨迹方程为__________,过点![]() 作倾斜角互补的两条直线,分别与圆心
作倾斜角互补的两条直线,分别与圆心![]() 的轨迹相交于
的轨迹相交于![]() ,
,![]() 两点,则直线
两点,则直线![]() 的斜率为__________.
的斜率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若以
两点,若以![]() ,
,![]() 为邻边的平行四边形
为邻边的平行四边形![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,求证:平行四边形
上,求证:平行四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
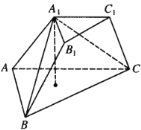
【题目】已知三棱台![]() 的下底面
的下底面![]() 是边长为2的正三角形,上地面
是边长为2的正三角形,上地面![]() 是边长为1的正三角形.
是边长为1的正三角形.![]() 在下底面的射影为
在下底面的射影为![]() 的重心,且
的重心,且![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .以
.以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,连接
,连接![]() 和
和![]() .
.
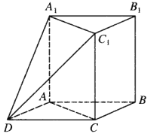
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com