
【题目】设集合A2n={1,2,3,…,2n}(n∈N* , n≥2).如果对于A2n的每一个含有m(m≥4)个元素的子集P,P中必有4个元素的和等于4n+1,称正整数m为集合A2n的一个“相关数”. (Ⅰ)当n=3时,判断5和6是否为集合A6的“相关数”,说明理由;
(Ⅱ)若m为集合A2n的“相关数”,证明:m﹣n﹣3≥0;
(Ⅲ)给定正整数n.求集合A2n的“相关数”m的最小值.
【答案】解:(Ⅰ)当n=3时,A6={1,2,3,4,5,6},4n+1=13,
①对于A6的含有5个元素的子集{2,3,4,5,6},
因为2+3+4+5>13,
所以5不是集合A6的“相关数”;
②A6的含有6个元素的子集只有{1,2,3,4,5,6},
因为1+3+4+5=13,
所以6是集合A6的“相关数”.
(Ⅱ)考察集合A2n的含有n+2个元素的子集B={n﹣1,n,n+1,…,2n},
B中任意4个元素之和一定不小于(n﹣1)+n+(n+1)+(n+2)=4n+2.
所以n+2一定不是集合A2n的“相关数”;
所以当m≤n+2时,m一定不是集合A2n的“相关数”,
因此若m为集合A2n的“相关数”,必有m≥n+3,
即若m为集合A2n的“相关数”,必有m﹣n﹣3≥0;
(Ⅲ)由(Ⅱ)得 m≥n+3,
先将集合A2n的元素分成如下n组:
Ci=(i,2n+1﹣i),(1≤n),
对A2n的任意一个含有n+3个元素的子集p,
必有三组 ![]() ,
, ![]() ,
, ![]() 同属于集合P,
同属于集合P,
再将集合A2n的元素剔除n和2n后,分成如下n﹣1组:
Dj=(j,2n﹣j),(1≤j≤n﹣1),
对于A2n的任意一个含有n+3个元素的子集P,必有一组 ![]() 属于集合P,
属于集合P,
这一组 ![]() 与上述三组
与上述三组 ![]() ,
, ![]() ,
, ![]() 中至少一组无相同元素,
中至少一组无相同元素,
不妨设 ![]() 与
与 ![]() 无相同元素.
无相同元素.
此时这4个元素之和为[i1+(2n+1﹣i1)+(2n﹣j4)]=4n+1,
所以集合A2n的“相关数”m的最小值为n+3
【解析】(Ⅰ)根据相关数的定义判断即可;(Ⅱ)根据相关数的定义得到m≤n+2时,m一定不是集合A2n的“相关数”,得到m≥n+3,从而证明结论;(Ⅲ)根据m≥n+3,将集合A2n的元素分成n组,对A2n的任意一个含有n+3个元素的子集p,必有三组 ![]() ,
, ![]() ,
, ![]() 同属于集合P,不妨设
同属于集合P,不妨设 ![]() 与
与 ![]() 无相同元素,此时这4个元素之和为[i1+(2n+1﹣i1)+(2n﹣j4)]=4n+1,从而求出m的最小值.
无相同元素,此时这4个元素之和为[i1+(2n+1﹣i1)+(2n﹣j4)]=4n+1,从而求出m的最小值.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
【题目】已知Sn是等差数列{an}的前n项和,且s6>s7>s5 , 给出下列五个命题:①d>0;②S11>0;③S12<0;④数列{Sn}中的最大项为S11;⑤|a5|>|a7|.其中正确命题的个数为( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班开展一次智力竞赛活动,共a,b,c三个问题,其中题a满分是20分,题b,c满分都是25分.每道题或者得满分,或者得0分.活动结果显示,全班同学每人至少答对一道题,有1名同学答对全部三道题,有15名同学答对其中两道题.答对题a与题b的人数之和为29,答对题a与题c的人数之和为25,答对题b与题c的人数之和为20.则该班同学中只答对一道题的人数是;该班的平均成绩是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x|x|.若存在x∈[1,+∞),使得f(x﹣2k)﹣k<0,则k的取值范围是( )
A.(2,+∞)
B.(1,+∞)
C.( ![]() ,+∞)
,+∞)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”). 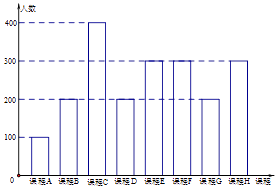
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组M”中选择F课程或G课程的同学,并且这些同学以自愿报名缴费的方式参加活动.选择F课程的学生中有x人参加科学营活动,每人需缴纳2000元,选择G课程的学生中有y人参加该活动,每人需缴纳1000元.记选择F课程和G课程的学生自愿报名人数的情况为(x,y),参加活动的学生缴纳费用总和为S元.
(ⅰ)当S=4000时,写出(x,y)的所有可能取值;
(ⅱ)若选择G课程的同学都参加科学营活动,求S>4500元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
(Ⅰ)求获得参赛资格的人数;
(Ⅱ)若大赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ![]() ,求甲在初赛中答题个数X的分布列及数学期望E(X)
,求甲在初赛中答题个数X的分布列及数学期望E(X)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( ) 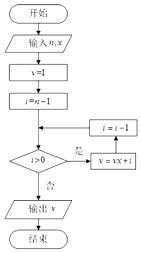
A.5
B.12
C.25
D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com