
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在定义域内单调递增,求实数
在定义域内单调递增,求实数![]() 的取值范围;
的取值范围;
(2)证明:方程![]() 有且只有一个实数根.
有且只有一个实数根.
【答案】(1) ![]() (2) 见解析
(2) 见解析
【解析】
(1)依题意,得![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 内恒成立;
内恒成立;
(2)方程![]() 有且只有一个实数根即证明函数
有且只有一个实数根即证明函数![]() 的图象与直线
的图象与直线![]() 有且只有一个交点.令
有且只有一个交点.令![]() ,研究其图象变化趋势即可.
,研究其图象变化趋势即可.
(1)由题得,函数![]() 的定义域为
的定义域为![]()
由![]() ,
,
得![]() ,
,
依题意,得![]() 恒成立,
恒成立,
所以![]() 在区间
在区间![]() 内恒成立,
内恒成立,
所以![]() .
.
而![]()
![]() ,当且仅当
,当且仅当![]() ,
,
即![]() 时,等号成立,
时,等号成立,
故![]() ,
,
因此实数![]() 的取值范围为
的取值范围为![]() .
.
(2)令![]() ,即
,即![]() ,
,
即![]()
![]() ,
,
也就是证明函数![]() 的图象与直线
的图象与直线![]() 有且只有一个交点.
有且只有一个交点.
由![]() ,
,
得![]()
![]()
记![]()
![]() ,
,
所以![]()
![]()
令![]()
![]() ,
,
当![]() 时,
时, ![]() ,
,![]() 在区间
在区间![]() 内单调递减;
内单调递减;
当![]() 时,
时, ![]() ,
,![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以当![]() 时,
时, ![]() 有有极小值
有有极小值![]()
![]() ,
,
故![]() ,
,
因此![]() 在区间
在区间![]() 内单调递增,
内单调递增,
又因为当![]() ,且
,且![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
因此函数![]() 的图象与直线
的图象与直线![]() 有且只有一个交点,
有且只有一个交点,
故方程![]() 有且只有一个实数根.
有且只有一个实数根.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以![]() 表示和为6的事件,求
表示和为6的事件,求![]() ;
;
(2)现连玩三次,若以![]() 表示甲至少赢一次的事件,
表示甲至少赢一次的事件,![]() 表示乙至少赢两次的事件,试问
表示乙至少赢两次的事件,试问![]() 与
与![]() 是否为互斥事件?为什么?
是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童玩具生产厂一车间计划每天生产遥控小车模型、遥控飞机模型、遥控火车模型这三种玩具共![]() 个,生产一个遥控小车模型需
个,生产一个遥控小车模型需![]() 分钟,生产一个遥控飞机模型需
分钟,生产一个遥控飞机模型需![]() 分钟,生产一个遥控火车模型需
分钟,生产一个遥控火车模型需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 分钟,若生产一个遥控小车模型可获利
分钟,若生产一个遥控小车模型可获利![]() 元,生产一个遥控飞机模型可获利
元,生产一个遥控飞机模型可获利![]() 元,生产一个遥控火车模型可获利
元,生产一个遥控火车模型可获利![]() 元,该公司合理分配生产任务可使每天的利润最大,则最大利润是__________元
元,该公司合理分配生产任务可使每天的利润最大,则最大利润是__________元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作:![]() .其中
.其中![]() 称为数组
称为数组![]() 的“元”,
的“元”,![]() 为
为![]() 的下标.如果数组
的下标.如果数组![]() 中的每个“元”都来自数组
中的每个“元”都来自数组![]() 中不同下标的“元”则称
中不同下标的“元”则称![]() 为
为![]() 的子数组.定义两个数组
的子数组.定义两个数组![]() ,
,![]() 的关系数为
的关系数为![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]() 的最大值及此时的数组
的最大值及此时的数组![]() ;
;
(2)若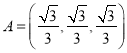 ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其
上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求![]() 的估计值;
的估计值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有120粒试验种子需要播种,现有两种方案:方案一:将120粒种子分种在40个坑内,每坑3粒;方案二:120粒种子分种在60个坑内,每坑2粒 如果每粒种子发芽的概率为0.5,并且,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种(每个坑至多补种一次,且第二次补种的种子颗粒同第一次).假定每个坑第一次播种需要2元,补种1个坑需1元;每个成活的坑可收货100粒试验种子,每粒试验种子收益1元.
(1)用![]() 表示播种费用,分别求出两种方案的
表示播种费用,分别求出两种方案的![]() 的数学期望;
的数学期望;
(2)用![]() 表示收益,分别求出两种方案的收益
表示收益,分别求出两种方案的收益![]() 的数学期望;
的数学期望;
(3)如果在某块试验田对该种子进行试验,你认为应该选择哪种方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月20日,辽宁省人民政府公布了“![]() ”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高.小明同学是2018级的学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了生物与化学近10大联考的成绩百分比排名数据x(如
”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高.小明同学是2018级的学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了生物与化学近10大联考的成绩百分比排名数据x(如![]() 的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的
的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的![]() )绘制茎叶图如下.
)绘制茎叶图如下.

则由图中数据生物学科联考百分比排名的![]() 分位数为________.从平均数的角度来看你认为小明更应该选择________.(填生物或化学)
分位数为________.从平均数的角度来看你认为小明更应该选择________.(填生物或化学)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com