
【题目】已知函数f(x)=lnx+x2 .
(Ⅰ)若函数g(x)=f(x)﹣ax在其定义域内为增函数,求实数a的取值范围;
(Ⅱ)在(Ⅰ)的条件下,若a>1,h(x)=e3x﹣3aexx∈[0,ln2],求h(x)的极小值;
(Ⅲ)设F(x)=2f(x)﹣3x2﹣kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n),且2x0=m+n.问:函数F(x)在点(x0 , F(x0))处的切线能否平行于x轴?若能,求出该切线方程;若不能,请说明理由.
【答案】解:(Ⅰ)g(x)=f(x)﹣ax=lnx+x2﹣ax, ![]()
由题意知,g′(x)≥0,对任意的x∈(0,+∞)恒成立,即 ![]()
又∵x>0, ![]() ,当且仅当
,当且仅当 ![]() 时等号成立
时等号成立
∴ ![]() ,可得
,可得 ![]()
(Ⅱ)由(Ⅰ)知, ![]() ,令t=ex,则t∈[1,2],则
,令t=ex,则t∈[1,2],则
h(t)=t3﹣3at, ![]()
由h′(t)=0,得 ![]() 或
或 ![]() (舍去),
(舍去),
∵ ![]() ,∴
,∴ ![]()
若 ![]() ,则h′(t)<0,h(t)单调递减;若
,则h′(t)<0,h(t)单调递减;若 ![]() ,则h′(t)>0,h(t)单调递增
,则h′(t)>0,h(t)单调递增
∴当 ![]() 时,h(t)取得极小值,极小值为
时,h(t)取得极小值,极小值为 ![]()
(Ⅲ)设F(x)在(x0,F(x0))的切线平行于x轴,其中F(x)=2lnx﹣x2﹣kx
结合题意,有 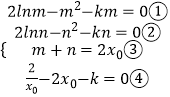
①﹣②得 ![]()
所以 ![]() ,由④得
,由④得 ![]()
所以 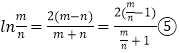
设 ![]() ,⑤式变为
,⑤式变为 ![]()
设 ![]() ,
, ![]()
所以函数 ![]() 在(0,1)上单调递增,
在(0,1)上单调递增,
因此,y<y|u=1=0,即 ![]() ,也就是
,也就是 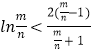 此式与⑤矛盾
此式与⑤矛盾
所以F(x)在(x0,F(x0))的切线不能平行于x轴
【解析】(1)根据f(x)的解析式,写出g(x)的解析式,求导,由于g(x)单调递增,可得出![]() 在
在![]() 恒大于零,进行参变分离求出a的取值范围;(2)令
恒大于零,进行参变分离求出a的取值范围;(2)令![]() 进行换元,讨论t的范围,求出h(t)的单调区间,找出函数的最小值;(3)先设F(x)在
进行换元,讨论t的范围,求出h(t)的单调区间,找出函数的最小值;(3)先设F(x)在![]() 的切线平行于x轴由题意得出方程组,换元研究单调性,证出在(0,1)上成立,从而与题设矛盾,故函数F(x)在
的切线平行于x轴由题意得出方程组,换元研究单调性,证出在(0,1)上成立,从而与题设矛盾,故函数F(x)在![]() 处的切线不平行于x轴。
处的切线不平行于x轴。


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“x∈R,使得x2+x+1<0”的否定是:“x∈R,x2+x+1>0”
B.命题“若x2﹣3x+2=0,则x=1或x=2”的否命题是:“若x2﹣3x+2=0,则x≠1或x≠2”
C.直线l1:2ax+y+1=0,l2:x+2ay+2=0,l1∥l2的充要条件是 ![]()
D.命题“若x=y,则sinx=siny”的逆否命题是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ax2(a∈R),y=f(x)的图象连续不间断.
(1)求函数y=f(x)的单调区间;
(2)当a=1时,设l是曲线y=f(x)的一条切线,切点是A,且l在点A处穿过函数y=f(x)的图象(即动点在点A附近沿曲线y=f(x)运动,经过点A时,从l的一侧进入另一侧),求切线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图扇形AOB是一个观光区的平面示意图,其中∠AOB的圆心角为 ![]() ,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,
,半径OA为1Km,为了便于游客观光休闲,拟在观光区内铺设一条从入口A到出口B的观光道路,道路由圆弧AC、线段CD及线段BD组成.其中D在线段OB上,且CD∥AO,设∠AOC=θ,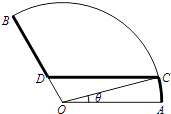
(1)用θ表示CD的长度,并写出θ的取值范围.
(2)当θ为何值时,观光道路最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,﹣ ![]() <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 , 2)和(x0+2π,﹣2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 , 2)和(x0+2π,﹣2).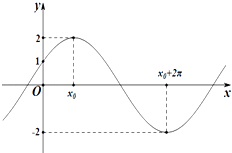
(1)求函数f(x)的解析式;
(2)若锐角θ满足f(2θ+ ![]() )=
)= ![]() ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,且该几何体的顶点都在同一球面上,则该几何体的外接球的表面积为( )
A.32π
B.48π
C.50π
D.64π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆C1:x2+y2=1经过伸缩变换 ![]() 后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ=
后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ= ![]()
(1)求曲线C2的直角坐标方程及直线l的直角坐标方程;
(2)在C2上求一点M,使点M到直线l的距离最小,并求出最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的左、右焦点分别为F1(﹣c,0)、F2(c,0),过椭圆中心的弦PQ满足|PQ|=2,∠PF2Q=90°,且△PF2Q的面积为1.
的左、右焦点分别为F1(﹣c,0)、F2(c,0),过椭圆中心的弦PQ满足|PQ|=2,∠PF2Q=90°,且△PF2Q的面积为1.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l不经过点A(0,1),且与椭圆交于M,N两点,若以MN为直径的圆经过点A,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com