
【题目】设s,t是不相等的两个正数,且s+slnt=t+tlns,则s+t﹣st的取值范围为( )
A.(﹣∞,1)B.(﹣∞,0)C.(0,+∞)D.(1,+∞)
科目:高中数学 来源: 题型:
【题目】在平面多边形![]() 中,四边形
中,四边形![]() 是边长为2的正方形,四边形
是边长为2的正方形,四边形![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,
的中点,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
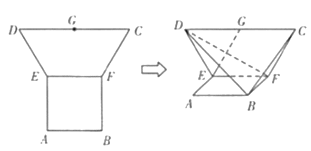
(1)求证:![]() 面
面![]() ;
;
(2)求![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取![]() 名工人,将他们随机分成两组,每组
名工人,将他们随机分成两组,每组![]() 人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:
人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:![]() )绘制了如图所示的茎叶图(茎为十位数,叶为个位数):
)绘制了如图所示的茎叶图(茎为十位数,叶为个位数):
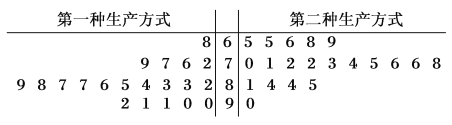
(1)根据茎叶图,估计两种生产方式完成任务所需时间至少![]() 分钟的概率,并对比两种生产方式所求概率,判断哪种生产方式的效率更高?
分钟的概率,并对比两种生产方式所求概率,判断哪种生产方式的效率更高?
(2)将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: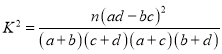
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆柱的轴截面ABCD是边长为2的正方形,点P是圆弧CD上的一动点(不与C,D重合),点Q是圆弧AB的中点,且点P,Q在平面ABCD的两侧.
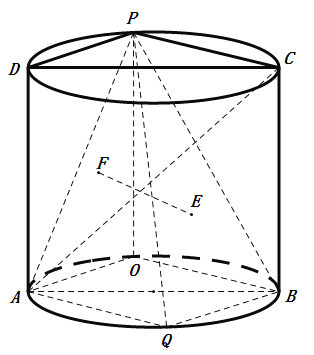
(1)证明:平面PAD⊥平面PBC;
(2)设点P在平面ABQ上的射影为点O,点E,F分别是△PQB和△POA的重心,当三棱锥P﹣ABC体积最大时,回答下列问题.
(i)证明:EF∥平面PAQ;
(ii)求平面PAB与平面PCD所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
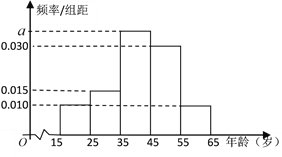
(1)求![]() 的值;
的值;
(2)求出样本的平均数(同一组数据用该区间的中点值作代表);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求第2组中抽到
人进行问卷调查,求第2组中抽到![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com