
【题目】若函数![]() 在区间
在区间![]() 上递减,则a的取值范围是______.
上递减,则a的取值范围是______.
【答案】![]()
【解析】
由题意,在区间(﹣∞,1]上,a的取值需令真数x2﹣2ax+1+a>0,且函数u=x2﹣2ax+1+a在区间(﹣∞,1]上应单调递减,这样复合函数才能单调递减.
令u=x2﹣2ax+1+a,则f(u)=lgu,
配方得u=x2﹣2ax+1+a=(x﹣a)2 ﹣a2+a+1,故对称轴为x=a,如图所示:
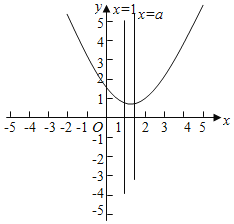
由图象可知,当对称轴a≥1时,u=x2﹣2ax+1+a在区间(﹣∞,1]上单调递减,
又真数x2﹣2ax+1+a>0,二次函数u=x2﹣2ax+1+a在(﹣∞,1]上单调递减,
故只需当x=1时,若x2﹣2ax+1+a>0,
则x∈(﹣∞,1]时,真数x2﹣2ax+1+a>0,
代入x=1解得a<2,所以a的取值范围是[1,2)
故答案为:![]()


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当点
,当点![]() 在
在![]() 的图像上移动时,点
的图像上移动时,点![]() 在函数
在函数![]() 的图像上移动,
的图像上移动,
(1)若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 也在
也在![]() 图像上,求
图像上,求![]() 的值。
的值。
(2)求函数![]() 的解析式。
的解析式。
(3)当![]() ,令
,令![]() ,求
,求![]() 在
在![]() 上的最值。
上的最值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点. 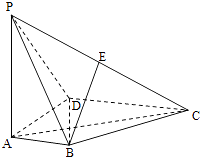
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F﹣AB﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() ,
,![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值;
的值;
(2)当函数![]() 在定义域内不单调时,求证:
在定义域内不单调时,求证:![]() ;
;
(3)是否存在实数![]() ,使得对任意
,使得对任意![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.(参考数据:
的值;若不存在,请说理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①存在实数![]() ,使
,使![]() ; ②函数
; ②函数![]() 是偶函数;
是偶函数;
③若![]() 是第一象限的角,且
是第一象限的角,且![]() ,则
,则![]() ;
;
④直线![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
⑤函数![]() 的图像关于点
的图像关于点![]() 成对称中心图形.
成对称中心图形.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两个旅游景点之间有一条5km的直线型水路,一艘游轮以![]() 的速度航行时
的速度航行时![]() 考虑到航线安全要求
考虑到航线安全要求![]() ,每小时使用的燃料费用为
,每小时使用的燃料费用为![]() 万元
万元![]() 为常数,且
为常数,且![]() ,其他费用为每小时
,其他费用为每小时![]() 万元.
万元.
![]() 若游轮以
若游轮以![]() 的速度航行时,每小时使用的燃料费用为
的速度航行时,每小时使用的燃料费用为![]() 万元,要使每小时的所有费用不超过
万元,要使每小时的所有费用不超过![]() 万元,求x的取值范围;
万元,求x的取值范围;
![]() 求该游轮单程航行所需总费用的最小值.
求该游轮单程航行所需总费用的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com