
【题目】双曲线 ![]() 的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
(1)若l的倾斜角为 ![]() ,
, ![]() 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ![]() ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率.
科目:高中数学 来源: 题型:
【题目】用另一种形式表示下列集合:
(1){绝对值不大于3的整数};
(2){所有被3整除的数};
(3){x|x=|x|,x∈Z且x<5};
(4){x|(3x-5)(x+2)(x2+3)=0,x∈Z}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)设f(x)、g(x)、h(x)是定义域为R的三个函数,对于命题:①若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是增函数,则f(x)、g(x)、h(x)均是增函数;②若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是以T为周期的函数,则f(x)、g(x)、h(x)均是以T为周期的函数,下列判断正确的是( )
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块正方形菜地 ![]() ,
, ![]() 所在直线是一条小河,收货的蔬菜可送到
所在直线是一条小河,收货的蔬菜可送到 ![]() 点或河边运走。于是,菜地分为两个区域
点或河边运走。于是,菜地分为两个区域 ![]() 和
和 ![]() ,其中
,其中 ![]() 中的蔬菜运到河边较近,
中的蔬菜运到河边较近, ![]() 中的蔬菜运到
中的蔬菜运到 ![]() 点较近,而菜地内
点较近,而菜地内 ![]() 和
和 ![]() 的分界线
的分界线 ![]() 上的点到河边与到
上的点到河边与到 ![]() 点的距离相等,现建立平面直角坐标系,其中原点
点的距离相等,现建立平面直角坐标系,其中原点 ![]() 为
为 ![]() 的中点,点
的中点,点 ![]() 的坐标为(1,0),如图
的坐标为(1,0),如图
(1)求菜地内的分界线 ![]() 的方程
的方程
(2)菜农从蔬菜运量估计出 ![]() 面积是
面积是 ![]() 面积的两倍,由此得到
面积的两倍,由此得到 ![]() 面积的“经验值”为
面积的“经验值”为 ![]() 。设
。设 ![]() 是
是 ![]() 上纵坐标为1的点,请计算以
上纵坐标为1的点,请计算以 ![]() 为一边、另一边过点
为一边、另一边过点 ![]() 的矩形的面积,及五边形
的矩形的面积,及五边形 ![]() 的面积,并判断哪一个更接近于
的面积,并判断哪一个更接近于 ![]() 面积的经验值
面积的经验值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示 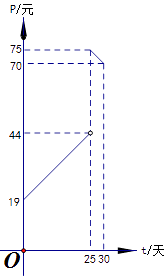
(1)写出销售价格P(元)和时间t(天)的函数解析式;
(2)若日销售量Q(件)与时间t(天)的函数关系是Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
A.各月的平均最低气温都在0℃以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20℃的月份有5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com