练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，正四棱锥底面的四个顶点，，，在球的同一个大圆上，点在球面上，且已知．

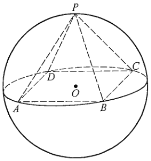
    （1）求球的表面积；

    （2）设为中点，求异面直线与所成角的大小．

    【答案】（1）（2）

    【解析】

    （1）由题意可知，平面，并且是半径，由体积求出半径，然后求出球的表面积．

    （2）以，，为，，轴建立空间直角坐标系，写出各点的坐标，进一步求出的坐标，利用向量的数量积公式求出的夹角余弦，得到异面直线与所成角的大小．

    解：（1）解：如图，正四棱锥底面的四个顶点，，，在球的同一个大圆上，点在球面上，底面，，，，

    所以，，

    球的表面积是

    （2）以，，为，，轴建立空间直角坐标系，则

    ，0，，，0，，，2，，，0，，，1，，

    ，，

    所以

    所以异面直线与所成角的余弦值为．

    所以异面直线与所成角的大小为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和为，且满足，，，.

    （1）求数列{an}的通项公式；

    （2）记，.

    ①求Tn；

    ②求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图中有一个信号源和五个接收器．接收器与信号源在同一个串联线路中时，就能接收到信号，否则就不能接收到信号．若将图中左端的六个接线点随机地平均分成三组，将右端的六个接线点也随机地平均分成三组，再把所得六组中每组的两个接线点用导线连接，则这五个接收器能同时接收到信号的概率是（ ）．

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.
    (1)求该函数的最小正周期和最小值;
    (2)若,求该函数的单调递增区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】厂家在产品出厂前，需对产品做检验．厂家将一批产品发给商家时，商家按合同规定也需随机抽取一定数量的产品做检验，以决定是否接收这批产品．

    （1）若厂家库房中的每件产品合格的概率为0.8，从中任意取出4件进行检验，求至少有1件是合格品的概率；

    （2）若厂家发给商家20件产品，其中有3件不合格．按合同规定该商家从中任取2件，都进行检验，只有2件都合格时才接收这批产品，否则拒收．求该商家拒收这批产品的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知复数，，，，，满足，．

    （1）若所对应点在圆上，求所对应点的轨迹；

    （2）是否存在这样的直线，对应点在上，所对应点也在直线上？若存在，求出所有这些直线；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱柱中，，，，，是棱的中点，平面与直线相交于点.

    （1）证明：直线平面.

    （2）求二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】房屋的天花板上点处有一光源，在地面上的射影为，在地面上放置正棱锥，底面接触地面．已知正四棱锥的高为，底面的边长为，与正方形的中心的距离为，又长为，则棱锥影子（不包括底面）的面积的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年4月8日零时正式解除离汉通道管控，这标志着封城76天的武汉打开城门了.在疫情防控常态下，武汉市有序复工复产复市，但是仍然不能麻痹大意，仍然要保持警惕，严密防范、慎终如始.为科学合理地做好小区管理工作，结合复工复产复市的实际需要，某小区物业提供了，两种小区管理方案，为了了解哪一种方案最为合理有效，物业随机调查了50名男业主和50名女业主，每位业主对，两种小区管理方案进行了投票（只能投给一种方案），得到下面的列联表：

    方案

    方案

    男业主

    35

    15

    女业主

    25

    25

    （1）分别估计，方案获得业主投票的概率；

    （2）判断能否有95％的把握认为投票选取管理方案与性别有关.

    附：.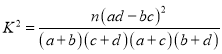

    查看答案和解析>>

    同步练习册答案