
已知函数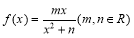 , 在
, 在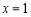 处取得极小值2.
处取得极小值2.
(1)求函数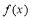 的解析式;
的解析式;
(2)求函数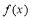 的极值;
的极值;
(3)设函数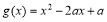 , 若对于任意
, 若对于任意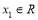 ,总存在
,总存在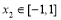 , 使得
, 使得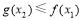 , 求实数
, 求实数 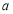 的取值范围.
的取值范围.
(1)函数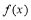 的解析式为
的解析式为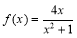 ;(2)
;(2)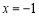 时,函数
时,函数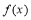 有极小值-2;当
有极小值-2;当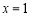 时,函数
时,函数 有极大值2 ;(3)a的取值范围是(-∞,-1]∪[ 3,+∞).
有极大值2 ;(3)a的取值范围是(-∞,-1]∪[ 3,+∞).
【解析】
试题分析:(1)根据函数在极值处导函数为0,极小值为2联立方程组即可求得m,n;(2)由(1)求得函数解析式,对函数求导且让导函数为0,即可求得极大值和极小值;(3)依题意只需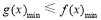 即可,当
即可,当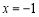 时,函数
时,函数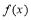 有最小值-2 ,即对任意
有最小值-2 ,即对任意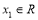 总存在
总存在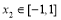 ,使得
,使得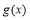 的最小值不大于-2 ;而
的最小值不大于-2 ;而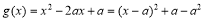 ,分
,分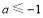 、
、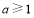 、
、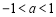 三种情况讨论即可.
三种情况讨论即可.
试题解析:(1)∵函数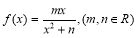 在
在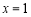 处取得极小值2,∴
处取得极小值2,∴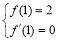 1分
1分
又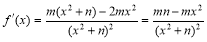 ∴
∴
由②式得m=0或n=1,但m=0显然不合题意 ∴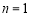 ,代入①式得m=4
,代入①式得m=4
∴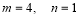 2分
2分
经检验,当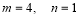 时,函数
时,函数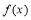 在
在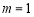 处取得极小值2
处取得极小值2
∴函数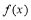 的解析式为
的解析式为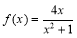 4分
4分
(2)∵函数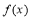 的定义域为
的定义域为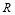 且由(1)有
且由(1)有 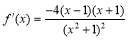
令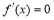 ,解得:
,解得: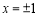
∴当x变化时,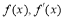 的变化情况如下表:
的变化情况如下表:
x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| — | 0 | + | 0 | — |
| 减 | 极小值-2 | 增 | 极大值2 | 减 |
∴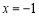 时,函数
时,函数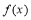 有极小值-2;当
有极小值-2;当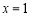 时,函数
时,函数 有极大值2 8分
有极大值2 8分
(3)依题意只需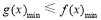 即可.
即可.
∵函数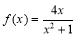 在
在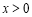 时,
时,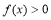 ;在
;在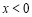 时,
时,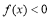 且
且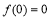
∴ 由(2)知函数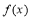 的大致图象如图所示:
的大致图象如图所示:
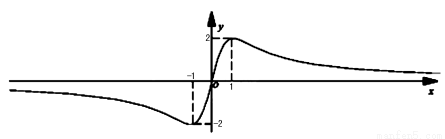
∴当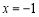 时,函数
时,函数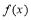 有最小值-2 10分
有最小值-2 10分
又对任意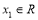 总存在
总存在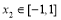 ,使得
,使得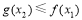 ∴当
∴当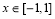 时,
时,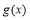 的最小值不大于-2
的最小值不大于-2
又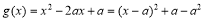
①当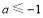 时,
时,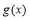 的最小值为
的最小值为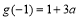 ∴
∴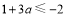 得
得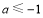 ;
;
②当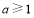 时,
时,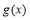 的最小值为
的最小值为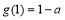 ∴
∴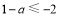 得
得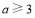 ;
;
③当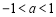 时,
时,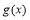 的最小值为
的最小值为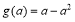 ∴
∴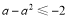 得
得 或
或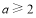
又∵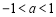 ∴此时a不存在
∴此时a不存在
综上所述,a的取值范围是(-∞,-1]∪[3,+∞). 13分
考点:导数的应用、函数思想、分类讨论思想.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4.1练习卷(解析版) 题型:填空题
自由落体运动的物体下降距离h和时间t的关系式为h=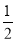 gt2,t=2时的瞬时速度为19.6,则g=________.
gt2,t=2时的瞬时速度为19.6,则g=________.
查看答案和解析>>
科目:高中数学 来源:2015届湖南张家界市高二上学期期末联考理科数学试卷(解析版) 题型:填空题
假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 1.4 | 2.3 | 3.1 | 3.7 | 4.5 |
若由资料可知y对x呈线性相关关系,且线性回归方程为=a+bx,其中已知b=1.23,请估计使用年限为20年时,维修费用约为________.
查看答案和解析>>
科目:高中数学 来源:2015届湖南张家界市高二上学期期末联考理科数学试卷(解析版) 题型:选择题
从装有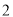 只红球和
只红球和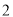 只黒球的口袋内任取
只黒球的口袋内任取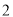 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A.至少有一个黒球与都是黒球 B.至少有一个黒球与都是红球
C.至少有一个黒球与至少有 只红球 D.恰有
只红球 D.恰有 只黒球与恰有
只黒球与恰有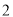 只黒球
只黒球
查看答案和解析>>
科目:高中数学 来源:2015届湖南张家界市高二上学期期末联考文科数学试卷(解析版) 题型:填空题
在计算机语言中有一种函数y=int(x)叫做取整函数(也叫高斯函数),它表示不超过x的最大整数,如int(0.9)=0,int(3.14)=3,已知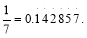 令
令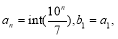 令当n>1时,
令当n>1时,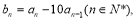 则
则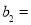 ,
, 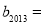 .
.
查看答案和解析>>
科目:高中数学 来源:2015届湖南张家界市高二上学期期末联考文科数学试卷(解析版) 题型:选择题
对具有线性相关关系的变量 ,
,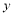 测得一组数据如下表:
测得一组数据如下表:
x | 2 | 4 | 5 | 6 | 8 |
y | 20 | 40 | 60 | 80 | 100 |
根据上表,利用最小二乘法得到它们的回归直线方程为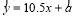 .据此模型预测
.据此模型预测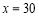 时,
时, 的估计值为( )
的估计值为( )
A. 320 B. 320.5 C. 322.5 D. 321.5
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测理数学试卷(解析版) 题型:填空题
如果随机变量X~N(-1,σ2),且P(-3≤X≤-1)=0.4,则P(X≥1)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com