
分析 (1)去绝对值,需对x进行讨论,分别求解.
(2)利用分析的方法,得出函数的单调性.
(3)对不等式化简整理可得:m≥-32t-1,把恒成立问题转换为最值问题,利用单调性求闭区间最值即可.
解答 解:(1)当x<0时,f(x)=3x-$\frac{1}{{3}^{-x}}$=3x-3x=0,
∴f(x)=2无解;
当x≥0时,f(x)=3x-$\frac{1}{{3}^{x}}$=2,
解得x=log3(1+$\sqrt{2}$);
(2)当x>0时,f(x)=3x-$\frac{1}{{3}^{x}}$,
∵3x在(0,+∞)上递增,
∴$\frac{1}{{3}^{x}}$在(0,+∞)上递减,
∴-$\frac{1}{{3}^{x}}$在(0,+∞)上递增,
∴f(x)=3x-$\frac{1}{{3}^{x}}$在(0,+∞)上递增,
(3)∵3tf(2t)+mf(t)≥0
∴3t(32t-$\frac{1}{{3}^{2t}}$)+m(3t-$\frac{1}{{3}^{t}}$)≥0,
∴3t(3t+$\frac{1}{{3}^{t}}$)+m≥0,
∴m≥-32t-1,
令g(t)=-32t-1,在t∈[$\frac{1}{2}$,1]上递减,
∴g(t)的最大值为g($\frac{1}{2}$)=-4,
∴m≥-4.
点评 考查了抽象函数的讨论问题,函数单调性的判断和恒成立问题.属于基础题型,应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-∞,1) | C. | (-∞,4] | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
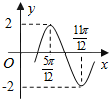 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数表达式为y=2sin(2x-$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com