
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
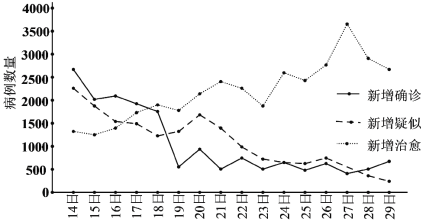
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数大于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于![]()
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】近年来,政府相关部门引导乡村发展旅游的同时,鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响,甲,乙两同学一起收集6家农户的数据,进行回归分折,得到两个回归摸型:模型①:![]() ,模型②:
,模型②: ![]() ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表:
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
(1)将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
(2)视残差![]() 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
附: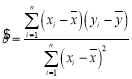 ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥C﹣ABNM中,四边形ABNM的边长均为2,△ABC为正三角形,MB![]() ,MB⊥NC,E,F分别为MN,AC中点.
,MB⊥NC,E,F分别为MN,AC中点.
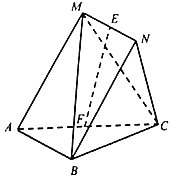
(Ⅰ)证明:MB⊥AC;
(Ⅱ)求直线EF与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
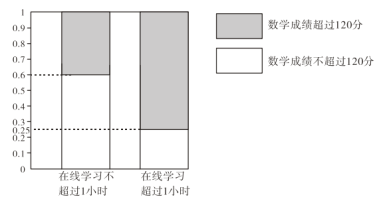
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知l,m是平面![]() 外的两条不同直线.给出下列三个论断:
外的两条不同直线.给出下列三个论断:
①l⊥m;②m∥![]() ;③l⊥
;③l⊥![]() .
.
以其中的两个论断作为条件,余下的一个论断作为结论,则三个命题中正确命题的个数为( )个.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
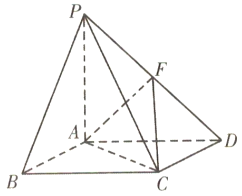
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (其中
(其中![]() ,m,n为常数)
,m,n为常数)
(1)当![]() 时,对
时,对![]() 有
有![]() 恒成立,求实数n的取值范围;
恒成立,求实数n的取值范围;
(2)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,函数
,函数![]() 的零点为
的零点为![]() ,求所有满足
,求所有满足![]() 的整数k的和.
的整数k的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com