
【题目】已知无穷数列{an}(an∈Z)的前n项和为Sn,记S1,S2,…,Sn中奇数的个数为bn.
(1)若an=n,请写出数列{bn}的前5项;
(2)求证:“a1为奇数,ai(i=2,3,4,…)为偶数”是“数列{bn}是单调递增数列”的充分不必要条件;
(3)若ai=bi,i=1,2,3,…,求数列{an}的通项公式.
【答案】(1) b1=1,b2=2,b3=2,b4=2,b5=3.(2)证明见解析;(3) an=0
【解析】
(1)当![]() 时,
时,![]() ,由此能写出数列
,由此能写出数列![]() 的前5项
的前5项
(2)先证充分性,推导出![]() ,从而数列
,从而数列![]() 是单调递增数列;再证不必要性,当数列
是单调递增数列;再证不必要性,当数列![]() 中只有
中只有![]() 是奇数,其余项都是偶数时,
是奇数,其余项都是偶数时,![]() 为偶数,
为偶数,![]() (
(![]() )均为奇数,
)均为奇数,![]() ,数列
,数列![]() 是单调递增数列,由此能证明:“
是单调递增数列,由此能证明:“![]() 是奇数,
是奇数,![]() 为偶数”是“数列
为偶数”是“数列![]() 是单调递增数列”的充分不必要条件
是单调递增数列”的充分不必要条件
(3)当![]() 为奇数时,推导出
为奇数时,推导出![]() 不能为偶数;当
不能为偶数;当![]() 为偶数,推导出
为偶数,推导出![]() 不能是奇数,从而
不能是奇数,从而![]() 与
与![]() 同奇偶,由此得到
同奇偶,由此得到![]()
(1)当![]() 时,可知数列
时,可知数列![]() 是等差数列,则
是等差数列,则![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(2)证明:(充分性)
∵![]() 是奇数,
是奇数,![]() 为偶数,
为偶数,
∴对于任意![]() ,
,![]() 都是奇数,
都是奇数,
∴![]() ,
,
∴数列![]() 是单调递增数列
是单调递增数列
(不必要性)
当数列![]() 中只有
中只有![]() 是奇数,其余项都是偶数时,
是奇数,其余项都是偶数时,![]() 为偶数,
为偶数,![]() (
(![]() )均为奇数,
)均为奇数,
∴![]() ,数列
,数列![]() 是单调递增数列,
是单调递增数列,
∴“![]() 是奇数,
是奇数,![]() 为偶数”是“数列
为偶数”是“数列![]() 是单调递增数列”的不必要条件
是单调递增数列”的不必要条件
综上,“![]() 是奇数,
是奇数,![]() 为偶数”是“数列
为偶数”是“数列![]() 是单调递增数列”的充分不必要条件
是单调递增数列”的充分不必要条件
(3)(i)当![]() 为奇数时,若
为奇数时,若![]() 为偶数,
为偶数,
若![]() 是奇数,则
是奇数,则![]() 为奇数,∴
为奇数,∴![]() 为偶数,与
为偶数,与![]() 矛盾;
矛盾;
若![]() 为偶数,则
为偶数,则![]() 为偶数,∴
为偶数,∴![]() 为奇数,与
为奇数,与![]() 矛盾
矛盾
∴当![]() 为奇数时,
为奇数时,![]() 不能为偶数
不能为偶数
(ii)当![]() 为偶数,若
为偶数,若![]() 为奇数,
为奇数,
若![]() 为奇数,则
为奇数,则![]() 为偶数,∴
为偶数,∴![]() 为偶数,与
为偶数,与![]() 矛盾,
矛盾,
若![]() 为偶数,则
为偶数,则![]() 为奇数,∴
为奇数,∴![]() 为奇数,与
为奇数,与![]() 矛盾,
矛盾,
∴当![]() 为偶数时,
为偶数时,![]() 不能是奇数
不能是奇数
综上,![]() 与
与![]() 同奇偶,
同奇偶,
∵![]() 为偶数,且
为偶数,且![]() ,∴
,∴![]() ,
,
∵![]() ,且
,且![]() ,∴
,∴![]() ,
,
以此类推,得到![]()


科目:高中数学 来源: 题型:
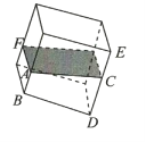
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中
(1)在等差数列![]() 中,
中,![]() 是
是![]() 的充要条件;
的充要条件;
(2)已知等比数列![]() 为递增数列,且公比为
为递增数列,且公比为![]() ,若
,若![]() ,则当且仅当
,则当且仅当![]() ;
;
(3)若数列![]() 为递增数列,则
为递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
(4)已知数列![]() 满足
满足![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]()
(5)若![]() 是等比数列
是等比数列![]() 的前
的前![]() 项的和,且
项的和,且![]() ;(其中
;(其中![]() 、
、![]() 是非零常数,
是非零常数,![]() ),则A+B为零.
),则A+B为零.
其中正确命题是_________(只需写出序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂以![]() 千克/小时的速度匀速生产某种产品(生产条件要求
千克/小时的速度匀速生产某种产品(生产条件要求![]() ),每小时可获得利润是
),每小时可获得利润是![]() 元.
元.
(1)要使生产该产品![]() 小时获得的利润不低于
小时获得的利润不低于![]() 元,求
元,求![]() 的取值范围;
的取值范围;
(2)要使生产![]() 千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是______
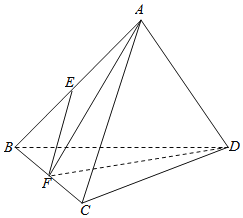
①异面直线AB与CD所成角为90°;
②直线AB与平面BCD所成角为60°;
③直线EF∥平面ACD
④平面AFD⊥平面BCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线
是两条不同的直线![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:(1)若
是三个不同的平面,给出下列四个命题:(1)若![]() ,
,![]() ,那么
,那么![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;(3)若
;(3)若![]() ,
,![]() ,那么
,那么![]() ;(4)若
;(4)若![]() ,
,![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.(1)(2)B.(2)(3)C.(1)(3)D.(2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com