
���� ��I����an=��$\sqrt{S_n}+\sqrt{{S_{n-1}}}$����n��2��n��N*�����ɵ�Sn-Sn-1=��$\sqrt{S_n}+\sqrt{{S_{n-1}}}$����n��2��n��N*��������������{an}��ǰn���ΪSn���ɵ�$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1������֤����
��II���ɣ�I���ɵã�$\sqrt{{S}_{n}}$=1+��n-1��=n��Sn=n2������an=Sn-Sn-1���ɵó���
��III�����á�������͡����������еĵ����Լ��ɵó���
��� ��I��֤������an=��$\sqrt{S_n}+\sqrt{{S_{n-1}}}$����n��2��n��N*����
��Sn-Sn-1=��$\sqrt{S_n}+\sqrt{{S_{n-1}}}$����n��2��n��N*����
����������{an}��ǰn���ΪSn����$\sqrt{S_n}+\sqrt{{S_{n-1}}}$��0��
��$\sqrt{{S}_{n}}$-$\sqrt{{S}_{n-1}}$=1��
��{$\sqrt{S_n}\}$�ǵȲ����У�����Ϊ1������Ϊ1��
��II���⣺�ɣ�I���ɵã�$\sqrt{{S}_{n}}$=1+��n-1��=n��
��Sn=n2��
��an=Sn-Sn-1=n2-��n-1��2=2n-1��
��III���⣺bn=$\frac{4n}{{a_n^2•a_{n+1}^2}}$=$\frac{4n}{��2n-1��^{2}��2n+1��^{2}}$=$\frac{1}{2}[\frac{1}{��2n-1��^{2}}-\frac{1}{��2n+1��^{2}}]$��
������{bn}��ǰn���ΪTn=$\frac{1}{2}$$[��1-\frac{1}{{3}^{2}}��+��\frac{1}{{3}^{2}}-\frac{1}{{5}^{2}}��$+��+$��\frac{1}{��2n-1��^{2}}-\frac{1}{��2n+1��^{2}}��]$
=$\frac{1}{2}[1-\frac{1}{��2n+1��^{2}}]$$��\frac{1}{2}$��
��ʹ��Tn��$\frac{m}{10}$��������n��N*����������$\frac{1}{2}��\frac{m}{10}$�����m��5��
���ʹ��Tn��$\frac{m}{10}$��������n��N*����������С������m=5��
���� ���⿼�������еĵ��ƹ�ϵ����������ͷ��������Ȳ����е�ͨ�ʽ�����еĵ����ԣ�������������������������������е��⣮


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭������һ�и߶��϶ο�һ��ѧ�������Ծ��������棩 ���ͣ�ѡ����
Բ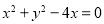 ��Բ������Ͱ뾶�ֱ�Ϊ�� ��
��Բ������Ͱ뾶�ֱ�Ϊ�� ��
A����0,2����2 B����2,0����2 C����-2,0����4 D����2,0����4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{2}$ | B�� | $\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{{\sqrt{3}}}{4}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{5}{6}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com