
【题目】如图,在长方体![]() 中,
中, ![]() 与平面
与平面![]() 及平面
及平面![]() 所成角分别为
所成角分别为![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 的中点,且
的中点,且![]() .
.
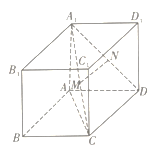
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据中位线定理可得MN∥CD,由长方体的性质可得CD⊥平面![]() ,从而可得结果;(2)以AB,AD,
,从而可得结果;(2)以AB,AD, ![]() 所在直线为x,y,z轴建立空间直角坐标系
所在直线为x,y,z轴建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 与平面
与平面![]() 的的一个法向量,根据空间向量夹角余弦公式及同角三角函数之间的关系,可得结果.
的的一个法向量,根据空间向量夹角余弦公式及同角三角函数之间的关系,可得结果.
试题解析:(1)证明:在长方体![]() 中,
中,
因为![]() ,所以
,所以![]() 为
为![]() 的中位线,
的中位线,
所以MN∥CD,
又因为CD⊥平面![]() ,
,
所以MN⊥平面![]() .
.
(2)解:在长方体![]() 中,因为CD⊥平面
中,因为CD⊥平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角,
所成的角,
即![]() =
=![]() ,
,
又因为![]() ⊥平面
⊥平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角,
所成的角,
即![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() =
=![]() ,
, ![]() ,
,
如图2,分别以AB,AD, ![]() 所在直线为x,y,z轴建立空间直角坐标系
所在直线为x,y,z轴建立空间直角坐标系![]() ,
,
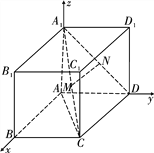
∴A(0,0,0),D(0,2,0), ![]() ,
, ![]() ,C(2,2,0),B(2,0,0),
,C(2,2,0),B(2,0,0),
在正方形ABCD中,BD⊥AC,
∴![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
, ![]() ,
,
所以有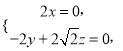
∴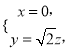 取z=1,
取z=1,
得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设二面角![]() 的大小为
的大小为![]() ,
,
则![]() .
.
∴![]() .
.
【方法点晴】本题主要考查线面垂直的判定、利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点, ![]() 是坐标原点,
是坐标原点, ![]() ,过
,过![]() 作
作![]() 的垂线交椭圆于
的垂线交椭圆于![]() ,
, ![]() 两点,
两点, ![]() 的面积为
的面积为![]() .
.

(1)求该椭圆的标准方程;
(2)若直线![]() 与上下半椭圆分别交于点
与上下半椭圆分别交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的面积取得最大值时直线
的面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到9这9个数字中任取3个偶数和3个奇数,组成无重复数字的六位数,
(1)有多少个偶数?
(2)若奇数排在一起且偶数排在一起,这样的六位数有多少个?
(3)若三个偶数不能相邻,这样的六位数有多少个?
(4)若三个偶数从左到右的排练顺序必须由大到小,这样的六位数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知6只小白鼠有1只被病毒感染,需要通过对其化验病毒![]() 来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒
来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒![]() ,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒
,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒![]() ,则在另外一组中逐个进行化验.
,则在另外一组中逐个进行化验.
(1)求依据方案乙所需化验恰好为2次的概率.
(2)首次化验化验费为10元,第二次化验化验费为8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的分布列,并估计用方案甲平均需要体验费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (x∈R).
(x∈R).
(1)求函数f(x)的值域;
(2)①判断函数f(x)的奇偶性;②用定义判断函数f(x)的单调性;
(3)解不等式f(1﹣m)+f(1﹣m2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
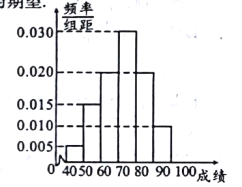
【题目】2017年《诗词大会》火爆荧屏,某校为此举办了一场主题为“爱诗词、爱祖国”的诗词知识竞赛,从参赛的全体学生中抽出60人的成绩(满分100分)作为样本.对这60名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() 分组,得到如图所示的频率分布直方图.
分组,得到如图所示的频率分布直方图.
(Ⅰ)若同一组数据用该组区间的中点值代表,估计参加这次知识竞赛的学生的平均成绩;
(Ⅱ)估计参加这次知识竞赛的学生成绩的中位数(结果保留一位小数);
(Ⅲ)若规定80分以上(含80分)为优秀,用频率估计概率,从全体参赛学生中随机抽取3名,记其中成绩优秀的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com