
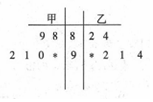
 在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”
在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”分析 (Ⅰ)先分别求出甲班前5位选手的总分和乙班前5位选手的总分,由此利用列举法能求出乙班总分超过甲班的概率.
(Ⅱ)①分别求出甲、乙两班平均分和方差,由此能求出甲班选手间的实力相当,相差不大,乙班选手间实力悬殊,差距较大.
②ξ的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
解答 解:(Ⅰ)甲班前5位选手的总分为88+89+90+91+92=450,
乙班前5位选手的总分为82+84+92+91+94=443,
若乙班总分超过甲班,则甲、乙两班第六位选手的成绩可分别为:
(90,98),(90,99),(91,99),共三个,
∴乙班总分超过甲班的概率为p=$\frac{3}{10×10}$=$\frac{3}{100}$.
(Ⅱ)①甲班平均分为$\overline{{x}_{甲}}$=$\frac{1}{6}$(88+89+90+91+92+90)=90,
乙班平均数为$\overrightarrow{{x}_{乙}}$=$\frac{1}{6}$(82+84+92+91+94+97)=90,
甲班方差为S2甲=$\frac{1}{6}$(22+12+12+22)=$\frac{5}{3}$,
乙班方差为S2乙=$\frac{1}{6}$(82+62+22+12+42+72)=$\frac{85}{3}$,
两班的平均分相同,但甲班选手的方差小于乙班,
故甲班选手间的实力相当,相差不大,乙班选手间实力悬殊,差距较大.
②ξ的可能取值为0,1,2,3,4,
P(ξ=0)=$\frac{{C}_{4}^{2}{C}_{2}^{2}}{{C}_{6}^{2}{C}_{6}^{2}}$=$\frac{6}{225}$,
P(ξ=1)=$\frac{{C}_{2}^{1}{C}_{4}^{1}{C}_{2}^{2}+{C}_{4}^{2}{C}_{4}^{1}{C}_{2}^{1}}{{C}_{6}^{2}{C}_{6}^{2}}$=$\frac{56}{225}$,
P(ξ=2)=$\frac{{C}_{2}^{1}{C}_{4}^{1}{C}_{4}^{1}{C}_{2}^{1}+{C}_{4}^{2}{C}_{4}^{2}}{{C}_{6}^{2}{C}_{6}^{2}}$=$\frac{101}{225}$,
P(ξ=3)=$\frac{{C}_{2}^{2}{C}_{4}^{1}{C}_{2}^{1}+{C}_{2}^{1}{C}_{4}^{1}{C}_{4}^{2}}{{C}_{6}^{2}{C}_{6}^{2}}$=$\frac{56}{225}$,
P(ξ=4)=$\frac{{C}_{2}^{2}{C}_{4}^{2}}{{C}_{6}^{2}{C}_{6}^{2}}$=$\frac{6}{225}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{6}{225}$ | $\frac{56}{225}$ | $\frac{101}{225}$ | $\frac{56}{225}$ | $\frac{6}{225}$ |
点评 本题考查茎叶图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com