
【题目】已知点![]() 在双曲线
在双曲线![]()
![]() (
(![]() ,
,![]() )上,且双曲线的一条渐近线的方程是
)上,且双曲线的一条渐近线的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两个不同的点,若以线段
两个不同的点,若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
【答案】(1)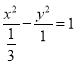 ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)要求双曲线的标准方程,必须找到关于![]() 的两个等式,题中一条渐近线方程为
的两个等式,题中一条渐近线方程为![]() ,说明
,说明![]() ,这是一个等式,点
,这是一个等式,点![]() 在双曲线上,那么此点坐标适合双曲线方程,代入进去又可得到一个等式,这样可解得
在双曲线上,那么此点坐标适合双曲线方程,代入进去又可得到一个等式,这样可解得![]() ;(2)直线与双曲线有两个不同的交点,直接把直线方程与双曲线方程联立方程组,此方程组有两解,方法是消去一个元
;(2)直线与双曲线有两个不同的交点,直接把直线方程与双曲线方程联立方程组,此方程组有两解,方法是消去一个元![]() ,得到关于
,得到关于![]() 的二次方程,此方程是二次方程有两个不等的实根,则
的二次方程,此方程是二次方程有两个不等的实根,则![]() ;(3)题设条件说明
;(3)题设条件说明![]() ,如果设
,如果设![]() ,则有
,则有![]() ,
,![]() 可用
可用![]() 表示出来,而
表示出来,而![]() 在(2)中可用
在(2)中可用![]() 表示出来,代入刚才的等式,得到
表示出来,代入刚才的等式,得到![]() 的方程,可解得
的方程,可解得![]() .
.
试题解析:(1)由题知,有
解得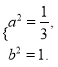
因此,所求双曲线![]() 的方程是
的方程是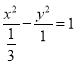 .
.
(2)∵直线![]() 过点
过点![]() 且斜率为
且斜率为![]() ,
,
∴直线![]() :
:![]() .
.
联立方程组![]() 得
得![]() .
.
又直线![]() 与双曲线
与双曲线![]() 有两个不同交点,
有两个不同交点,
∴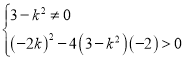
解得![]() .
.
(3)设交点为![]() ,由(2)可得
,由(2)可得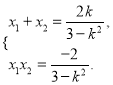
又以线段![]() 为直径的圆经过坐标原点,
为直径的圆经过坐标原点,
因此,![]() 为坐标原点).
为坐标原点).
于是,![]() 即
即![]() ,
,![]() ,
,
![]() ,解得
,解得![]() .
.
又![]() 满足
满足![]() ,且
,且![]() ,
,
所以,所求实数![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某疾病控制中心为了研究某种病毒的抗体,将这种病毒感染源放人含40个小白鼠的封闭容器中进行感染,未感染病毒的小白鼠说明已经产生了抗体,已知小白鼠对这种病毒产生抗体的概率为![]() .现对40个小白鼠进行抽血化验,为了检验出所有产生该种病毒抗体的小白鼠,设计了下面的检测方案:按
.现对40个小白鼠进行抽血化验,为了检验出所有产生该种病毒抗体的小白鼠,设计了下面的检测方案:按![]() (
(![]() ,且
,且![]() 是40的约数)个小白鼠平均分组,并将抽到的同组的
是40的约数)个小白鼠平均分组,并将抽到的同组的![]() 个小白鼠每个抽取的一半血混合在一起化验,若发现该病毒抗体,则对该组的
个小白鼠每个抽取的一半血混合在一起化验,若发现该病毒抗体,则对该组的![]() 个小白鼠抽取的另一半血逐一化验,记
个小白鼠抽取的另一半血逐一化验,记![]() 为某组中含有抗体的小白鼠的个数.
为某组中含有抗体的小白鼠的个数.
(1)若![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(2)为减少化验次数的期望值,试确定![]() 的大小.
的大小.
(参考数据: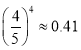 ,
,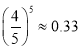 ,
,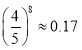 ,
, ,
,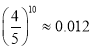 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,AC、BD交于点O,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
中,底面ABCD为矩形,AC、BD交于点O,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.

(1)求证:BD⊥平面PAC;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比.药物释放完毕后,
(小时)成正比.药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:

(1)求从药物释放开始,每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米空气的含药量降到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到进教室?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是圆柱的直径,
是圆柱的直径,![]() 是圆柱的母线,
是圆柱的母线,![]() ,
,![]() ,点
,点![]() 是圆柱底面圆周上的点.
是圆柱底面圆周上的点.
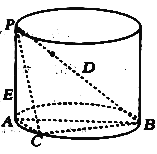
(1)求三棱锥![]() 体积的最大值;
体积的最大值;
(2)若![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点,点
的三等分点,点![]() 是线段
是线段![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
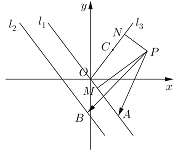
【题目】如图,已知直线![]() 和直线
和直线![]() ,射线
,射线![]() 的一个法向量为
的一个法向量为![]() ,点
,点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的动点,直线
上的动点,直线![]() 和
和![]() 之间的距离为2,
之间的距离为2,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() 、
、![]() ,动点
,动点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 、
、![]() 的两个斜率存在,分别记为
的两个斜率存在,分别记为![]() 、
、![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹有两个交点
的轨迹有两个交点![]() 、
、![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com