练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】关于的说法，正确的是( )

    A.展开式中的二项式系数之和为2048

    B.展开式中只有第6项的二项式系数最大

    C.展开式中第6项和第7项的二项式系数最大

    D.展开式中第6项的系数最小

    【答案】ACD

    【解析】

    根据二项式系数的性质即可判断选项A；

    由为奇数可知，展开式中二项式系数最大项为中间两项，据此即可判断选项BC；

    由展开式中第6项的系数为负数，且其绝对值最大即可判断选项D.

    对于选项A：由二项式系数的性质知，的二项式系数之和为，故选项A正确；

    因为的展开式共有项，中间两项的二项式系数最大，即第6项和第7项的二项式系数最大，故选项C正确，选项B错误；

    因为展开式中第6项的系数是负数，且绝对值最大，所以展开式中第6项的系数最小，故选项D正确；

    故选：ACD

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某摸球游戏的规则如下：从装有5个大小、形状完全相同的小球的盒中摸球（其中3个红球、2个黄球），每次摸一个球记录颜色并放回，若摸出红球记1分，摸出黄球记2分．

    （1）求“摸球三次得分为5分”的概率；

    （2）设ξ为摸球三次所得的分数，求随机变量ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解中学生课外阅读情况，现从某中学随机抽取名学生，收集了他们一年内的课外阅读量（单位：本）等数据，以下是根据数据绘制的统计图表的一部分.

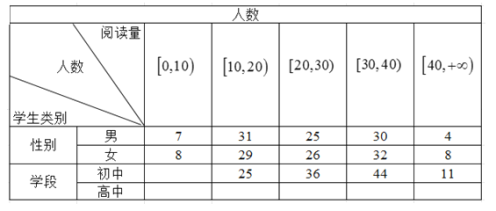
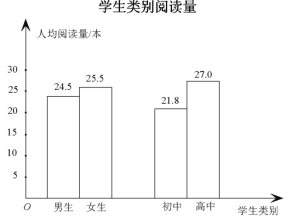
    下面有四个推断：

    ①这名学生阅读量的平均数可能是本；

    ②这名学生阅读量的分位数在区间内；

    ③这名学生中的初中生阅读量的中位数一定在区间内；

    ④这名学生中的初中生阅读量的分位数可能在区间内.

    所有合理推断的序号是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以函数为基本素材，研究该函数的相关性质，取得部分研究成果如下：其中研究成果正确的是（ ）

    A.同学甲发现：函数的定义域为（﹣1，1），且f（x）是偶函数

    B.同学乙发现：对于任意的x∈（﹣1，1），都有

    C.同学丙发现：对于任意的a，b∈（﹣1，1），都有

    D.同学丁发现：对于函数定义域内任意两个不同的实数x1，x2，总满足

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.（是自然对数的底数）

    （1）求的单调递减区间；

    （2）若函数，证明在上只有两个零点.（参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）lg．

    （1）判断并证明函数f（x）的单调性；

    （2）解关于x的不等式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，．

    若，解不等式；

    若不等式对一切实数x恒成立，求实数a的取值范围；

    若，解不等式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表中的数据是一次阶段性考试某班的数学、物理原始成绩：

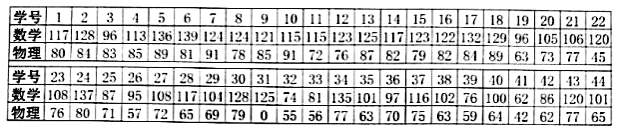
    用这44人的两科成绩制作如下散点图：

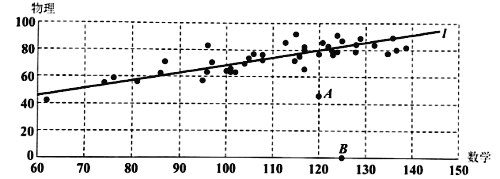
    学号为22号的同学由于严重感冒导致物理考试发挥失常，学号为31号的同学因故未能参加物理学科的考试，为了使分析结果更客观准确，老师将两同学的成绩（对应于图中两点）剔除后，用剩下的42个同学的数据作分析，计算得到下列统计指标：

    数学学科平均分为110.5，标准差为18.36，物理学科的平均分为74，标准差为11.18，数学成绩

    与物理成绩的相关系数为，回归直线（如图所示）的方程为.

    （1）若不剔除两同学的数据，用全部44人的成绩作回归分析，设数学成绩与物理成绩的相关系数为，回归直线为，试分析与的大小关系，并在图中画出回归直线的大致位置；

    （2）如果同学参加了这次物理考试，估计同学的物理分数（精确到个位）；

    （3）就这次考试而言，学号为16号的同学数学与物理哪个学科成绩要好一些？（通常为了比较某个学生不同学科的成绩水平，可按公式统一化成标准分再进行比较，其中为学科原始分，为学科平均分，为学科标准差）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业接到生产3000台某产品的三种部件的订单，每台产品需要这三种部件的数量分别为2,2,1（单位：件）,已知每个工人每天可生产A部件6件，或B部件3件，或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件，生产B部件的人数与生产A部件的人数成正比，比例系数为k（k为正整数）.

    （1）设生产部件的人数为，分别写出完成三种部件生产需要的时间；

    （2）假设这三种部件的生产同时开工，试确定正整数k的值，使完成订单任务的时间最短，并给出时间最短时具体的人数分组方案.

    查看答案和解析>>

    同步练习册答案