
【题目】如图,已知三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
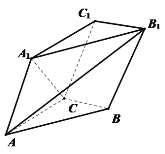
(1)证明:![]()
![]() ;
;
(2)设![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连结![]() .由菱形得对角线垂直,再由已知及面面垂直的性质定理得线面垂直
.由菱形得对角线垂直,再由已知及面面垂直的性质定理得线面垂直![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,从而
,从而![]() ,于是证得线面垂直后再得线线垂直;
,于是证得线面垂直后再得线线垂直;
(2)取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,证得
,证得![]() 与
与![]() 都垂直后,以
都垂直后,以![]() 为原点,
为原点,![]() 为正方向建立空间直角坐标系,写出各点坐标,求出平面的法向量,则法向量夹角得二面角,注意要判断二面角是锐角还是钝角.
为正方向建立空间直角坐标系,写出各点坐标,求出平面的法向量,则法向量夹角得二面角,注意要判断二面角是锐角还是钝角.
(1)连结![]() .
.
∵![]() ,四边形
,四边形![]() 为菱形,∴
为菱形,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]()
![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]()
![]()
(2)取![]() 的中点为
的中点为![]() ,连结
,连结![]() .
.
∵![]() ,四边形
,四边形![]() 为菱形,
为菱形,![]() ,∴
,∴![]() ,
,![]() .
.
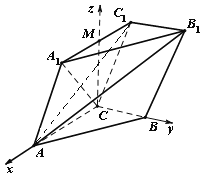
又由(1)知![]() ,以
,以![]() 为原点,
为原点,![]() 为正方向建立空间直角坐标系,如图.
为正方向建立空间直角坐标系,如图.
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() (0,0,0),
(0,0,0),![]() (1,0,
(1,0,![]() ),
),![]() (2,0,0),
(2,0,0),![]() (0,1,0),
(0,1,0),![]() (-1,1,
(-1,1,![]() ).
).
由(1)知,平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,∴
,∴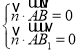 .
.
∵![]() ,
,![]() ,∴
,∴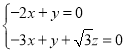 .
.
令![]() ,得
,得![]() ,即
,即![]() .
.
∴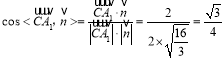 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]()


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC, ![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
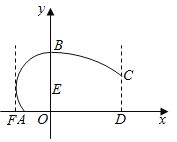
【题目】某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示,曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ;曲线
;曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.假定拟建体育馆的高
的半径.假定拟建体育馆的高![]() (单位:米,下同).
(单位:米,下同).
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 的长度;
的长度;
(2)若要求体育馆侧面的最大宽度![]() 不超过
不超过![]() 米,求
米,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
②四边形![]() 一定是平行四边形;
一定是平行四边形;
③平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
④四边形![]() 的面积有最大值.
的面积有最大值.
其中所有正确结论的序号为( )
A.①④B.②③C.①②④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能为正方形;
有可能为正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④平面![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
其中所有正确结论的序号为( )
A.①②B.②③④C.①④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,![]() =λ
=λ![]() .
.
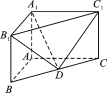
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1- A1C1-D的大小为60°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
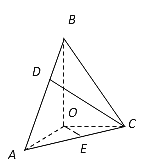
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com