分析:(1)将n=5代入(x+1)n中,变形可得[(x-1)+1]5,则a2为其展开式中(x-1)2的系数,由二项式定理可得答案;
(2)由于与二项式有关,故可采用赋值法.取x=1,则a0=2n,从而可求Sn,再用数学归纳法证明即可,只不过需注意假设n=k时成立,求当n=k+1时,Sn增加2k+1-2k=2k项.
解答:解:(1)根据题意,(x+1)
5=[2+(x-1)]
5=a
0+a
1(x-1)+a
2(x-1)
2+…+a
5(x-1)
5,
则a
2(x-1)
2=C
522
5-2(x-1)
2故a
2=80;
(2)在:(x+1)
n=a
0+a
1(x-1)+a
2(x-1)
2+a
3(x-1)
3+…+a
n(x-1)
n中,
令x=1,可得a
0=2
n,
则
Sn=1+++…+=1
+++…+,
①当n=2时,S
n=1
+++…+=1+
+,显然1<S
n≤2
故当n=2时,满足
<Sn≤n②假设当n=k(k>2,k∈N)时,满足
<Sn≤n,
即
<S
k=1+
++…+
≤k成立,
当n=k+1(k>2,k∈N)时,
S
k+1=1+
++…+
+
+…+
>++…+
>++…+
>+×(
+
…+
)
>+=
S
k+1=1+
++…+
+
+…+
≤k+
+…+
≤k+1
故当n=k+1(k>2,k∈N)时,
<S
k+1≤k+1
综合①②可知,
<Sn≤n,n∈N*,n≥2.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,同时考查了数学归纳法,属于中档题.



 阅读快车系列答案
阅读快车系列答案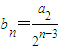 ,Tn=b2+b3+b4+…+bn.试用数学归纳法证明:当n≥2时,
,Tn=b2+b3+b4+…+bn.试用数学归纳法证明:当n≥2时,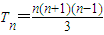 .
.