
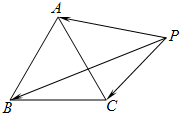
 如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且
如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且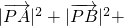
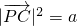 (a为常数).下列结论中,正确的是
(a为常数).下列结论中,正确的是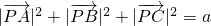 化为关于x、y、a的式子,化简整理可得x2+(y-
化为关于x、y、a的式子,化简整理可得x2+(y- )2=
)2= (a-1),讨论a的取值范围,可得当a>1时方程表示以点(0,
(a-1),讨论a的取值范围,可得当a>1时方程表示以点(0, )为圆心,半径r=
)为圆心,半径r=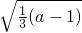 的圆,满足条件的点P有无数个,可知只有C项符合题意.
的圆,满足条件的点P有无数个,可知只有C项符合题意.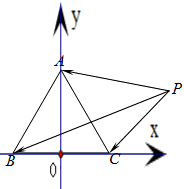 解:以BC所在直线为x轴,BC中点为原点,建立直角坐标系,如图所示
解:以BC所在直线为x轴,BC中点为原点,建立直角坐标系,如图所示 ,0),B(
,0),B( ,0),C(0,
,0),C(0, ),设P(x,y),可得
),设P(x,y),可得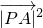 =x2+(y-
=x2+(y- )2,
)2,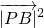 =(x+
=(x+ )2+y2,
)2+y2, =(x-
=(x- )2+y2
)2+y2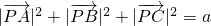
 )2+(x+
)2+(x+ )2+y2+(x-
)2+y2+(x- )2+y2=a
)2+y2=a y+
y+ -a=0,即x2+y2-
-a=0,即x2+y2- y+
y+ -
- =0
=0 )2=
)2= (a-1)…(1)
(a-1)…(1) ),恰好是正三角形的重心;
),恰好是正三角形的重心; )为圆心,半径为
)为圆心,半径为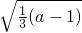 的圆
的圆

科目:高中数学 来源: 题型:
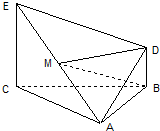 如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•徐州模拟)如图,△ABC是边长为2
(2012•徐州模拟)如图,△ABC是边长为2| 3 |
| AP |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•江苏三模)如图,△ABC是边长为2
(2012•江苏三模)如图,△ABC是边长为2| 3 |
| AP |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且|
(2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且|| PA |
| PB |
| PC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com