
ĄūĖâÄŋĄŋĩÚ23―ėķŽžū°ÂÔËŧáÓÚ2018Äę2ÔÂ9ČÕÖÁ2ÔÂ25ČÕÔÚšŦđúÆ―ēýūŲÐÐĢŽÆÚžäÕýÖĩÎŌĘÐŅ§ÐĢ·ÅšŪžŲĢŽšŪžŲ―áĘøšóĢŽÄģÐĢđĪŧáķÔČŦÐĢ―ĖÖ°đĪÔÚķŽžū°ÂÔËŧáÆÚžäÃŋĖėĘÕŋīąČČüŨŠēĨĩÄĘąžäŨũÁËŌŧīÎĩũēéĢŽĩÃĩ―ČįÏÂÆĩĘý·ÖēžąíĢš
ĘÕŋīĘąžäĢĻĩĨÎŧĢšÐĄĘąĢĐ |
|
|
|
|
|
|
ĘÕŋīČËĘý | 14 | 30 | 16 | 28 | 20 | 12 |
ĢĻ1ĢĐČô―ŦÃŋĖėĘÕŋīąČČüŨŠēĨĘąžäēŧĩÍÓÚ3ÐĄĘąĩÄ―ĖÖ°đĪķĻŌåΊĄ°ĖåÓýīïČËĄąĢŽ·ņÔōķĻŌåΊĄ°·ĮĖåÓýīïČËĄąĢŽĮëļųūÝÆĩĘý·ÖēžąíēđČŦ![]() ÁÐÁŠąíĢš
ÁÐÁŠąíĢš
| ÄÐ | ÅŪ | šÏžÆ |
ĖåÓýīïČË | 40 | ||
·ĮĖåÓýīïČË | 30 | ||
šÏžÆ |
ēĒÅÐķÏÄÜ·ņÓÐ![]() ĩÄ°ŅÎÕČÏΊļÃÐĢ―ĖÖ°đĪĘĮ·ņΊĄ°ĖåÓýīïČËĄąÓ륰ÐÔąðĄąÓÐđØĢŧ
ĩÄ°ŅÎÕČÏΊļÃÐĢ―ĖÖ°đĪĘĮ·ņΊĄ°ĖåÓýīïČËĄąÓ륰ÐÔąðĄąÓÐđØĢŧ
ĢĻ2ĢĐÔÚČŦÐĢĄ°ĖåÓýīïČËĄąÖаīÐÔąð·ÖēãģéŅųģéČĄ6ÃûĢŽÔŲīÓÕâ6ÃûĄ°ĖåÓýīïČËĄąÖÐŅĄČĄ2ÃûŨũķŽ°ÂŧáÖŠĘķ―ēŨų.žĮÆäÖÐÅŪÖ°đĪĩÄČËĘýΊ![]() ĢŽĮóĩÄ
ĢŽĮóĩÄ![]() ·ÖēžÁÐÓëĘýŅ§ÆÚÍû.
·ÖēžÁÐÓëĘýŅ§ÆÚÍû.
ļ―ąíž°đŦĘ―Ģš
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
Ąūīð°ļĄŋĢĻ1ĢĐžû―âÎöĢŧĢĻ2ĢĐžû―âÎö.
Ąū―âÎöĄŋĘÔĖâ·ÖÎöĢšĢĻ1ĢĐļųūÝĖâŌâĖîÐīÁÐÁŠąíĢŽžÆËãđÛēâÖĩĢŽķÔÕÕÁŲ―įÖĩĩÃģö―áÂÛĢŧ
ĢĻ2ĢĐÓÉĖâŌâÖŠģéČĄĩÄ6ÃûĄ°ĖåÓýīïČËĄąÖÐÓÐ4ÃûÄÐÖ°đĪĢŽ2ÃûÅŪÖ°đĪĢŽ
ËųŌÔ![]() ĩÄŋÉÄÜČĄÖĩΊ0ĢŽ1ĢŽ2.žÆËã
ĩÄŋÉÄÜČĄÖĩΊ0ĢŽ1ĢŽ2.žÆËã![]() ļÅÂĘÖĩĢŪĩÃĩ―
ļÅÂĘÖĩĢŪĩÃĩ―![]() ·ÖēžÁÐÓëĘýŅ§ÆÚÍû.
·ÖēžÁÐÓëĘýŅ§ÆÚÍû.
ĘÔĖâ―âÎöĢš
ĢĻ1ĢĐÓÉĖâŌâĩÃÏÂąíĢš
| ÄÐ | ÅŪ | šÏžÆ |
ĖåÓýīïČË | 40 | 20 | 60 |
·ĮĖåÓýīïČË | 30 | 30 | 60 |
šÏžÆ | 70 | 50 | 120 |
![]() ĩÄđÛēâÖĩΊ
ĩÄđÛēâÖĩΊ![]()
![]() .
.
ËųŌÔÓÐ![]() ĩÄ°ŅÎÕČÏΊļÃÐĢ―ĖÖ°đĪĘĮĄ°ĖåÓýīïČËĄąÓ륰ÐÔąðĄąÓÐđØ.
ĩÄ°ŅÎÕČÏΊļÃÐĢ―ĖÖ°đĪĘĮĄ°ĖåÓýīïČËĄąÓ륰ÐÔąðĄąÓÐđØ.
ĢĻ2ĢĐÓÉĖâŌâÖŠģéČĄĩÄ6ÃûĄ°ĖåÓýīïČËĄąÖÐÓÐ4ÃûÄÐÖ°đĪĢŽ2ÃûÅŪÖ°đĪĢŽ
ËųŌÔ![]() ĩÄŋÉÄÜČĄÖĩΊ0ĢŽ1ĢŽ2.
ĩÄŋÉÄÜČĄÖĩΊ0ĢŽ1ĢŽ2.
ĮŌ![]()
![]() ĢŽ
ĢŽ![]()
![]() ĢŽ
ĢŽ![]()
![]() ĢŽ
ĢŽ
ËųŌÔ![]() ĩÄ·ÖēžÁÐΊ
ĩÄ·ÖēžÁÐΊ
| 0 | 1 | 2 |
|
|
|
|
![]()
![]() .
.


 ĮáĮÉķáđÚÖÜēâÔÂŋžÖąÍĻÖÐŋžÏĩÁÐīð°ļ
ĮáĮÉķáđÚÖÜēâÔÂŋžÖąÍĻÖÐŋžÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĄũABCĩÄŌŧļöķĨĩãΊA(2,3)ĢŽÁ―ĖõļßËųÔÚÖąÏß·―ģĖΊxĢ2yĢŦ3Ģ―0šÍxĢŦyĢ4Ģ―0ĢŽĮóĄũABCČýąßËųÔÚÖąÏßĩÄ·―ģĖĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČôđØÓÚxĩÄēŧĩČĘ―e2xĐalnx![]() ašãģÉÁĒĢŽÔōĘĩĘýaĩÄČĄÖĩ·ķΧĘĮĢĻ ĢĐ
ašãģÉÁĒĢŽÔōĘĩĘýaĩÄČĄÖĩ·ķΧĘĮĢĻ ĢĐ
A.[0ĢŽ2e]B.ĢĻĐĄÞĢŽ2e]C.[0ĢŽ2e2]D.ĢĻĐĄÞĢŽ2e2]
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÄģÆóŌĩÓûŨöŌŧļö―éÉÜÆóŌĩ·ĒÕđĘ·ĩÄÃúÅÆĢŽÃúÅÆĩÄ―ØÃæÐÎŨīĘĮČįÍžËųĘūĩÄÉČÐÎŧ·Ãæ(ÓÉÉČÐÎ![]() ÍÚČĨÉČÐÎ
ÍÚČĨÉČÐÎ![]() šóđđģÉĩÄ)ĢŪŌŅÖŠ
šóđđģÉĩÄ)ĢŪŌŅÖŠ![]() ĢŽÏßķÎ
ĢŽÏßķÎ![]() ÓëŧĄ
ÓëŧĄ![]() ĄĒŧĄ
ĄĒŧĄ![]() ĩÄģĪķČÖŪšÍΊ
ĩÄģĪķČÖŪšÍΊ![]() ÃŨĢŽÔēÐÄ―ĮΊ
ÃŨĢŽÔēÐÄ―ĮΊ![]() ŧĄķČĢŪ
ŧĄķČĢŪ

(1)Įó![]() đØÓÚ
đØÓÚ![]() ĩÄšŊĘý―âÎöĘ―Ģŧ
ĩÄšŊĘý―âÎöĘ―Ģŧ
(2)žĮÃúÅÆĩÄ―ØÃæÃæŧýΊ![]() ĢŽĘÔÎĘ
ĢŽĘÔÎĘ![]() ČĄšÎÖĩĘąĢŽ
ČĄšÎÖĩĘąĢŽ![]() ĩÄÖĩŨîīóĢŋēĒĮóģöŨîīóÖĩĢŪ
ĩÄÖĩŨîīóĢŋēĒĮóģöŨîīóÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÄģīŽÔÚšĢÃæ![]() īĶēâĩÃĩÆËþ
īĶēâĩÃĩÆËþ![]() ÔÚąąÆŦķŦ
ÔÚąąÆŦķŦ![]() ·―ÏōĢŽÓë
·―ÏōĢŽÓë![]() Ïāūā
Ïāūā![]() šĢĀïĢŽēâĩÃĩÆËþ
šĢĀïĢŽēâĩÃĩÆËþ![]() ÔÚąąÆŦÎũ
ÔÚąąÆŦÎũ![]() ·―ÏōĢŽÓë
·―ÏōĢŽÓë![]() Ïāūā
Ïāūā![]() šĢĀïĢŽīŽÓÉ
šĢĀïĢŽīŽÓÉ![]() ÏōÕýąą·―Ïōš―ÐÐĩ―
ÏōÕýąą·―Ïōš―ÐÐĩ―![]() īĶĢŽēâĩÃĩÆËþ
īĶĢŽēâĩÃĩÆËþ![]() ÔÚÄÏÆŦÎũ
ÔÚÄÏÆŦÎũ![]() ·―ÏōĢŽÕâĘąĩÆËþ
·―ÏōĢŽÕâĘąĩÆËþ![]() Óë
Óë![]() ÏāūāķāÉŲšĢĀïĢŋ
ÏāūāķāÉŲšĢĀïĢŋ![]() ÔÚ
ÔÚ![]() ĩÄĘēÃī·―ÏōĢŋ
ĩÄĘēÃī·―ÏōĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() ĮŌ
ĮŌ![]() .
.
ĢĻ1ĢĐĮóĘĩĘý![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ2ĢĐÁî![]() ÔÚ
ÔÚ![]() ÉÏĩÄŨîÐĄÖĩΊ
ÉÏĩÄŨîÐĄÖĩΊ![]() ĢŽĮóÖĪĢš
ĢŽĮóÖĪĢš![]() .
.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
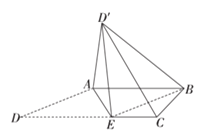
ĄūĖâÄŋĄŋČįÍžËųĘūĢŽŌŅÖŠËÄąßÐÎ![]() ĘĮÖą―ĮĖÝÐÎĢŽ
ĘĮÖą―ĮĖÝÐÎĢŽ![]() ĢŽ
ĢŽ![]() ĢŽÆäÖÐ
ĢŽÆäÖÐ![]() ĘĮ
ĘĮ![]() ÉÏĩÄŌŧĩãĢŽËÄąßÐÎ
ÉÏĩÄŌŧĩãĢŽËÄąßÐÎ![]() ĘĮÁâÐÎĢŽÂúŨã
ĘĮÁâÐÎĢŽÂúŨã![]() ĢŽŅØ
ĢŽŅØ![]() ―Ŧ
―Ŧ![]() ÕÛÆðĢŽĘđ
ÕÛÆðĢŽĘđ![]()
ĢĻ1ĢĐĮóÖĪĢšÆ―Ãæ![]() Æ―Ãæ
Æ―Ãæ![]()
ĢĻ2ĢĐĮóČýĀâŨķ![]() ĩÄĖåŧý.
ĩÄĖåŧý.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĖÆČýēĘĢŽÖÐđúđÅīúĖÕīÉÉÕÖÆđĪŌÕĩÄÕäÆ·ĢŽËüÎüČĄÁËÖÐđúđúŧĄĒĩņËÜĩČđĪŌÕÃĀĘõĩÄĖØĩãĢŽÔÚÖÐđúÎÄŧŊÖÐÕžÓÐÖØŌŠĩÄĀúĘ·ĩØÎŧĢŽÔÚÖÐđúĩÄĖÕīÉĘ·ÉÏÁôÏÂÁËÅĻÄŦÖØēĘĩÄŌŧąĘ.ĖÆČýēĘĩÄÉúēúÖÁ―ņŌŅÓÐ1300ķāÄęĩÄĀúĘ·ĢŽķÔĖÆČýēĘĩÄļīÖƚͷÂÖÆđĪŌÕĢŽÖÁ―ņŌēÓаŲÓāÄęĩÄĀúĘ·ĢŽÄģĖÕīÉģ§ÔÚÉúēúđýģĖÖÐĢŽķÔ·ÂÖÆ100žþđĪŌÕÆ·ēâĩÃÆäÖØÁŋ(ĩĨÎŧĢš![]() ) ĘýūÝĢŽ―ŦĘýūÝ·ÖŨéČįÏÂąíĢš
) ĘýūÝĢŽ―ŦĘýūÝ·ÖŨéČįÏÂąíĢš

ĢĻ1ĢĐÍģžÆ·―·ĻÖÐĢŽÍŽŌŧŨéĘýūÝģĢÓÃļÃŨéĮøžäĩÄÖÐĩãÖĩĢĻĀýČįĮøžä![]() ĩÄÖÐĩãÖĩĘĮ2.25ĢĐŨũΊīúąí.ūÝīËĢŽđĀžÆÕâ100ļöĘýūÝĩÄÆ―ūųÖĩĢŧ
ĩÄÖÐĩãÖĩĘĮ2.25ĢĐŨũΊīúąí.ūÝīËĢŽđĀžÆÕâ100ļöĘýūÝĩÄÆ―ūųÖĩĢŧ
ĢĻ2ĢĐļųūÝŅųąūĘýūÝĢŽŌÔÆĩÂĘŨũΊĢÂĘĢŽČôļÃĖÕīÉģ§ÉúēúÕâŅųĩÄđĪŌÕÆ·5000žþĢŽĘÔđĀžÆÖØÁŋÂäÔÚ![]() ÖÐĩÄžþĘýĢŧ
ÖÐĩÄžþĘýĢŧ
ĢĻ3ĢĐīÓĩÚŌŧŨéšÍĩÚÁųŨé6žþđĪŌÕÆ·ÖÐËæŧúģéČĄ2ļöđĪŌÕÆ·ĢŽĮóŌŧļöĀīŨÔĩÚŌŧŨéĢŽŌŧļöĀīŨÔĩÚÁųŨéĩÄļÅÂĘ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚÆ―ÃæÖą―ĮŨøąęÏĩ![]() ÖÐĢŽ
ÖÐĢŽ![]() ·ÖąðĘĮÍÖÔē
·ÖąðĘĮÍÖÔē![]() ĩÄŨóĄĒÓŌķĨĩã(ČįÍžËųĘū)ĢŽĩã
ĩÄŨóĄĒÓŌķĨĩã(ČįÍžËųĘū)ĢŽĩã![]() ÔÚÍÖÔēĩÄģĪÖá
ÔÚÍÖÔēĩÄģĪÖá![]() ÉÏÔËķŊĢŽĮŌ
ÉÏÔËķŊĢŽĮŌ![]() .ÉčÔē
.ÉčÔē![]() ĘĮŌÔĩã
ĘĮŌÔĩã![]() ΊÔēÐÄĢŽ
ΊÔēÐÄĢŽ![]() Ί°ëūķĩÄÔē.
Ί°ëūķĩÄÔē.
ĢĻ1ĢĐČô![]() ĢŽÔē
ĢŽÔē![]() šÍÍÖÔēÔÚĩÚŌŧÏóÏÞĩÄ―ŧĩãŨøąęΊ
šÍÍÖÔēÔÚĩÚŌŧÏóÏÞĩÄ―ŧĩãŨøąęΊ![]() ĢŽĮóÍÖÔēĩÄ·―ģĖĢŧ
ĢŽĮóÍÖÔēĩÄ·―ģĖĢŧ
ĢĻ2ĢĐČôÍÖÔēĩÄĀëÐÄÂĘΊ![]() ĢŽđýĩã
ĢŽđýĩã![]() ŨũŧĨÏāīđÖąĩÄÁ―ĖõÖąÏßĢŽ―ŧÍÖÔēÓÚP,QÁ―ĩãĢŽČôÖąÏßPQđýĩãMĢŽĮómĩÄÖĩĢĻÓÚŽ
ŨũŧĨÏāīđÖąĩÄÁ―ĖõÖąÏßĢŽ―ŧÍÖÔēÓÚP,QÁ―ĩãĢŽČôÖąÏßPQđýĩãMĢŽĮómĩÄÖĩĢĻÓÚŽ![]() ĩÄīúĘýĘ―ąíĘūĢĐĢŧ
ĩÄīúĘýĘ―ąíĘūĢĐĢŧ
ĢĻ3ĢĐĩąÔē![]() ÓëÍÖÔēÓÐĮŌ―öÓÐĩã
ÓëÍÖÔēÓÐĮŌ―öÓÐĩã![]() Ōŧļö―ŧĩãĘąĢŽĮó
Ōŧļö―ŧĩãĘąĢŽĮó![]() ĩÄÔËķŊ·ķΧĢĻÓÚŽ
ĩÄÔËķŊ·ķΧĢĻÓÚŽ![]() ĩÄīúĘýĘ―ąíĘūĢĐ.
ĩÄīúĘýĘ―ąíĘūĢĐ.
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com