练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列有关平面向量分解定理的四个命题：

    （1）一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基；

    （2）一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基；

    （3）平面向量的基向量可能互相垂直；

    （4）一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.

    其中正确命题的个数是（ ）

    A.1个B.2个C.3个D.4个

    【答案】B

    【解析】

    根据平面向量的基本定理，作为平面内所有向量的一组基底是两个向量不共线，由此对四个选项作出判断即可．

    一个平面内有无数多对不平行的向量可作为表示该平面所有向量的基，①错误，②正确；

    平面向量的基向量可能互相垂直，如正交基，③正确；

    平面内任一非零向量都可唯一地表示成该平面内两个互不平行向量的线性组合，

    如果是三个不共线的向量，表示法不唯一，④错误．

    综上，正确的命题是②③．

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦点和上顶点分别为，定义：为椭圆的“特征三角形”，如果两个椭圆的特征三角形是相似三角形，那么称这两个椭圆为“相似椭圆”，且特征三角形的相似比即为相似椭圆的相似比，已知点是椭圆的一个焦点，且上任意一点到它的两焦点的距离之和为4

    （1）若椭圆与椭圆相似，且与的相似比为2：1，求椭圆的方程.

    （2）已知点是椭圆上的任意一点，若点是直线与抛物线异于原点的交点，证明：点一定在双曲线上.

    （3）已知直线，与椭圆相似且短半轴长为的椭圆为，是否存在正方形，（设其面积为），使得在直线上，在曲线上？若存在，求出函数的解析式及定义域；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，椭圆的方程为，左右焦点分别为，，为短轴的一个端点，且的面积为.设过原点的直线与椭圆交于两点，为椭圆上异于的一点，且直线，的斜率都存在，.

    （1）求的值；

    （2）设为椭圆上位于轴上方的一点，且轴，、为曲线上不同于的两点，且，设直线与轴交于点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，角所对的边分别为．向量，，且

    （1）若，求角的值；

    （2）求角的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

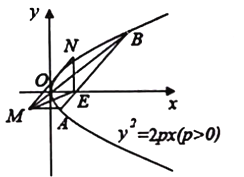
    【题目】如图，是坐标原点，过的直线分别交抛物线于、两点，直线与过点平行于轴的直线相交于点，过点与此抛物线相切的直线与直线相交于点.则（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数是定义在上的偶函数，且，当时，，则在区间内关于的方程解得个数为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，.

    （1）当时，求函数图象在处的切线方程；

    （2）若对任意，不等式恒成立，求的取值范围；

    （3）若存在极大值和极小值，且极大值小于极小值，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线过点，过点作直线与抛物线交于不同两点、，过作轴的垂线分别与直线、交于点、，其中为坐标原点.

    （1）求抛物线的方程；

    （2）写出抛物线的焦点坐标和准线方程；

    （3）求证：为线段的中点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若在区间上不是单调函数，求实数的范围；

    （2）若对任意，都有恒成立，求实数的取值范围；

    （3）当时，设，对任意给定的正实数，曲线上是否存在两点，，使得是以（为坐标原点）为直角顶点的直角三角形，而且此三角形斜边中点在轴上？请说明理由.

    查看答案和解析>>

    同步练习册答案