
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]()
![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
【答案】(1)调整前![]() 关于
关于![]() 的表达式为
的表达式为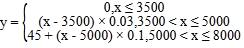 ,调整后
,调整后![]() 关于
关于![]() 的表达式为
的表达式为![]()
(2)![]()
(3)220元
【解析】
(1)对收入![]() 的范围分类,求出对应的表达式即可。
的范围分类,求出对应的表达式即可。
(2)列出7人中抽取2人共21种情况,找出不在同一收入人群的有12种结果,问题得解。
(3)计算出小红按调整起征点前应纳个税为![]() 元,小红按调整起征点后应纳个税为
元,小红按调整起征点后应纳个税为![]() 元,问题得解。
元,问题得解。
解:(1)调整前![]() 关于
关于![]() 的表达式为
的表达式为 ,
,
调整后![]() 关于
关于![]() 的表达式为
的表达式为![]() .
.
(2)由频数分布表可知从![]() 及
及![]() 的人群中按分层抽样抽取7人,其中
的人群中按分层抽样抽取7人,其中![]() 中占3人,分别记为
中占3人,分别记为![]() ,
,![]() 中占4人,分别记为1,2,3,4,再从这7人中选2人的所有组合有:
中占4人,分别记为1,2,3,4,再从这7人中选2人的所有组合有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,12,13,14,23,24,34,共21种情况,
,12,13,14,23,24,34,共21种情况,
其中不在同一收入人群的有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共12种,所以所求概率为
,共12种,所以所求概率为![]() .
.
(3)由于小红的工资、薪金等税前收入为7500元,
按调整起征点前应纳个税为![]() 元;
元;
按调整起征点后应纳个税为![]() 元,
元,
由此可知,调整起征点后应纳个税少交220元,
即个人的实际收入增加了220元,
所以小红的实际收入增加了220元.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆A:x2+y2+2x-15=0和定点B(1,0),M是圆A上任意一点,线段MB的垂直平分线交MA于点N,设点N的轨迹为C.
(Ⅰ)求C的方程;
(Ⅱ)若直线y=k(x-1)与曲线C相交于P,Q两点,试问:在x轴上是否存在定点R,使当k变化时,总有∠ORP=∠ORQ?若存在,求出点R的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() ,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,e]上的极值和最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
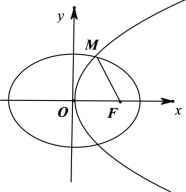
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在等腰梯形ABCD中,
,在等腰梯形ABCD中,![]() ,E,F分别为AB,CD的中点,
,E,F分别为AB,CD的中点,![]() ,M为DF中点.现将四边形BEFC沿EF折起,使平面
,M为DF中点.现将四边形BEFC沿EF折起,使平面![]() 平面AEFD,得到如图
平面AEFD,得到如图![]() 所示的多面体.在图
所示的多面体.在图![]() 中,
中,

(1)证明:![]() ;
;
(2)求二面角E-BC-M的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com