
【题目】已知圆锥曲线![]() (
( ![]() 是参数)和定点
是参数)和定点![]() , F1 , F2 是圆锥曲线的左、右焦点.
, F1 , F2 是圆锥曲线的左、右焦点.
(1)求经过点 F2 且垂直于直线 AF1 的直线 l 的参数方程;
(2)设 P 为曲线 C 上的动点,求 P 到直线 l 距离的取值范围.
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,M、N分别为CD和A1D1的中点,那么异面直线AM与BN 所成的角是( )
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x的不足近似值和过剩近似值分别为 ![]() 和
和 ![]() (a,b,c,d∈N*),则
(a,b,c,d∈N*),则 ![]() 是x的更为精确的不足近似值或过剩近似值.我们知道π=3.14159…,若令
是x的更为精确的不足近似值或过剩近似值.我们知道π=3.14159…,若令 ![]() <π<
<π< ![]() ,则第一次用“调日法”后得
,则第一次用“调日法”后得 ![]() 是π的更为精确的过剩近似值,即
是π的更为精确的过剩近似值,即 ![]() <π<
<π< ![]() ,若每次都取最简分数,那么第四次用“调日法”后可得π的近似分数为( )
,若每次都取最简分数,那么第四次用“调日法”后可得π的近似分数为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为梯形,PD⊥底面ABCD,AB∥CD,AD⊥CD,AD=AB=1,BC=![]() .
.
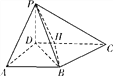
(Ⅰ)求证:平面PBD⊥平面PBC;
(Ⅱ)设H为CD上一点,满足![]() =2
=2![]() ,若直线PC与平面PBD所成的角的正切值为
,若直线PC与平面PBD所成的角的正切值为![]() ,求二面角H-PB-C的余弦值.
,求二面角H-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数是同一函数的是( )
①f(x)= ![]() 与g(x)=x
与g(x)=x ![]() ;
;
②f(x)=|x|与g(x)= ![]() ;
;
③f(x)=x0与g(x)= ![]() ;
;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①②③
B.①③④
C.②③④
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log23),c=f(0.20.6),则a,b,c的大小关系是( )
A.c<b<a
B.b<c<a
C.b<a<c
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)对一切实数x,y都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.
(1)求f(0)的值.
(2)求f(x)的解析式.
(3)已知a∈R,设P:当0<x< ![]() 时,不等式f(x)+3<2x+a恒成立;Q:当x∈[﹣2,2]时,g(x)=f(x)﹣ax是单调函数.如果满足P成立的a的集合记为A,满足Q成立的a的集合记为B,求A∩RB(R为全集).
时,不等式f(x)+3<2x+a恒成立;Q:当x∈[﹣2,2]时,g(x)=f(x)﹣ax是单调函数.如果满足P成立的a的集合记为A,满足Q成立的a的集合记为B,求A∩RB(R为全集).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某批次的某种灯泡![]() 个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命 (天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 的值;
的值;
(2)某人从这![]() 个灯泡中随机地购买了
个灯泡中随机地购买了![]() 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;
(3)某人从这批灯泡中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
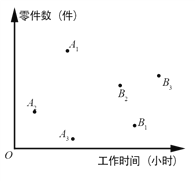
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的学科&网零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
①记Qi为第i名工人在这一天中加工的零件总数,则Q1,Q2,Q3中最大的是_________.
②记pi为第i名工人在这一天中平均每小时加工的零件数,则p1,p2,p3中最大的是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com