
【题目】已知动点P到点F(0,1)的距离比它到直线y=-3的距离少2.
(1)求点P的轨迹E的方程.
(2)过点F的两直线l1、l2分别与轨迹E交于A,B两点和C,D两点,且满足![]()
![]() =0,设M,N两点分别是线段AB,CD的中点,问直线MN是否恒过一定点,若经过,求定点的坐标;若不经过,请说明理由.
=0,设M,N两点分别是线段AB,CD的中点,问直线MN是否恒过一定点,若经过,求定点的坐标;若不经过,请说明理由.
【答案】(1)x2=4y;(2)(0,3)
【解析】
(1)由题意知动点P到点F的距离等于它到直线x=﹣1的距离,可得点P轨迹E是抛物线.(2)根据题意可知直线l1,l2都有斜率,设直线l1的方程为y=kx+1(k≠0),代入x2=4y,利用根与系数的关系可得M(2k,2k2+1),由![]()
![]() =0,可得
=0,可得![]() ,设出直线l2,可得N,写出直线MN的方程,化简即可得出结论.
,设出直线l2,可得N,写出直线MN的方程,化简即可得出结论.
(1)由题意知动点P到点F(0,1)的距离等于它到直线x=-1的距离相等,
所以点P的轨迹E是抛物线,轨迹方程是x2=4y
(2)根据题意可知,直线l1,l2都有斜率,
设直线l1的方程为y=kx+1(k≠0),代入x2=4y,得x2-4kx-4=0
设A(x1,y1),B(x2,y2),则![]()
∴M(2k,2k2+1)∵![]() ,∴
,∴![]()
设直线l2:![]() ,C(x3,y3),D(x4,y4),同理可得N
,C(x3,y3),D(x4,y4),同理可得N![]()
所以直线MN的方程为![]() ,化简得:y-3=
,化简得:y-3=![]() x,
x,
所以直线MN恒过定点(0,3).


科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,bsinA=![]() cosB.
cosB.
(1)求角B的大小;
(2)若b=2,△ABC的面积为![]() ,求a,c.
,求a,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数为5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)求在抽取的40名学生中月上网次数不少于15次的学生人数;
(Ⅲ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取2人,求至少抽到1名女生的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩是中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,而且优质品检验异常严格,检验方案是:先从烧制的这批唐三彩中任取 3件作检验,这3件唐三彩中优质品的件数记为![]() .如果
.如果![]() ,再从这批唐三彩中任取3件作检验,若都为优质品,则这批唐三彩通过检验;如果
,再从这批唐三彩中任取3件作检验,若都为优质品,则这批唐三彩通过检验;如果![]() ,再从这批唐三彩中任取1件作检验,若为优质品,则这批唐三彩通过检验;其他情况下,这批唐三彩都不能通过检验.假设这批唐三彩的优质品概率为
,再从这批唐三彩中任取1件作检验,若为优质品,则这批唐三彩通过检验;其他情况下,这批唐三彩都不能通过检验.假设这批唐三彩的优质品概率为![]() ,即取出的每件唐三彩是优质品的概率都为
,即取出的每件唐三彩是优质品的概率都为![]() ,且各件唐三彩是否为优质品相互独立.
,且各件唐三彩是否为优质品相互独立.
(1)求这批唐三彩通过优质品检验的概率;
(2)已知每件唐三彩的检验费用为100元,且抽取的每件唐三彩都需要检验,对这批唐三彩作质量检验所需的总费用记为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 任作一条与两条坐标轴都不垂直的直线,与椭圆
任作一条与两条坐标轴都不垂直的直线,与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8,当直线
的周长为8,当直线![]() 的斜率为
的斜率为![]() 时,
时, ![]() 与
与![]() 轴垂直.
轴垂直.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,总能使
,总能使![]() 平分
平分![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点F与长轴垂直的直线与椭圆在第一象限相交于点M,
,过右焦点F与长轴垂直的直线与椭圆在第一象限相交于点M,![]() .
.
(1)求椭圆C的标准方程;
(2)斜率为1的直线l与椭圆相交于B,D两点,若以线段BD为直径的圆恰好过坐标原点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD是边长为![]() 的正方形,平面PAC⊥底面ABCD,PA=PC=
的正方形,平面PAC⊥底面ABCD,PA=PC=![]()
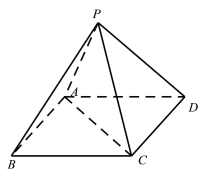
(1)求证:PB=PD;
(2)若点M,N分别是棱PA,PC的中点,平面DMN与棱PB的交点Q,则在线段BC上是否存在一点H,使得DQ⊥PH,若存在,求BH的长,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com