练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，直线l的参数方程为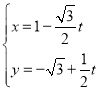（t为参数）.以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系.曲线C的极坐标方程为.

    （1）求直线l的普通方程及曲线C的直角坐标方程；

    （2）设点，直线l与曲线C相交于A，B两点，求的值.

    【答案】（1）l的普通方程为，曲线C的直角坐标方程为（2）

    【解析】

    （1）消去参数可得直线的普通方程，根据互化公式可得曲线的直角坐标方程．

    （2）根据直线的参数方程的几何意义可得．

    解：（1）消去参数t得直线l的普通方程为；

    因为，所以，

    因为，，

    所以曲线C的直角坐标方程为

    （2）易判断点是直线l上的点，设A，B两点所对应的参数分别为，

    将直线l的参数方程代入曲线C的直角坐标方程，得.

    其中，，.

    于是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在一条景观道的一端有一个半径为米的圆形摩天轮O，逆时针分钟转一圈，从处进入摩天轮的座舱，垂直于地面，在距离处米处设置了一个望远镜.

    （1）同学甲打算独自乘坐摩天轮，但是其母亲不放心，于是约定在登上摩天轮座舱分钟后，在座舱内向其母亲挥手致意，而其母亲则在望远镜中仔细观看.问望远镜的仰角应调整为多少度？（精确到1度）

    （2）在同学甲向其母亲挥手致意的同时，同一座舱的另一名乘客乙在拍摄地面上的一条绿化带，发现取景的视角恰为，求绿化带的长度（精确到1米）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在等腰直角中，，，点在线段上.

    (Ⅰ) 若，求的长；

    （Ⅱ）若点在线段上，且，问：当取何值时，的面积最小？并求出面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了解本校文、理科学生的学业水平模拟测试数学成绩情况，分别从理科班学生中随机抽取人的成绩得到样本甲，从文科班学生中随机抽取人的成绩得到样本乙，根据两个样本数据分别得到如下直方图：

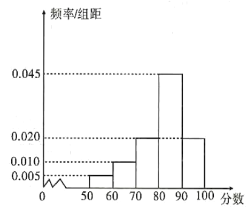
    甲样本数据直方图

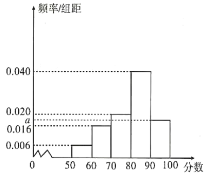
    乙样本数据直方图

    已知乙样本中数据在的有个.

    （1）求和乙样本直方图中的值；

    （2）试估计该校理科班学生本次模拟测试数学成绩的平均值和文科班学生本次模拟测试数学成绩的中位数（同一组中的数据用该组区间中点值为代表）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （1）求的单调区间；

    （2）在函数的图象上取两个不同的点，令直线AB的斜率

    为k，则在函数的图象上是否存在点，且，使得？若存

    在，求A，B两点的坐标，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市在争创文明城市过程中，为调查市民对文明出行机动车礼让行人的态度，选了某小区的100位居民调查结果统计如下：

    支持

    不支持

    合计

    年龄不大于45岁

    80

    年龄大于45岁

    10

    合计

    70

    100

    （1）根据已有数据，把表格数据填写完整；

    （2）能否在犯错误的概率不超过5%的前提下认为不同年龄段与是否支持文明出行机动车礼让行人有关？

    （3）已知在被调查的年龄小于25岁的支持者有5人，其中2人是教师，现从这5人中随机抽取3人，求至多抽到1位教师的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）试判断函数的单调性；

    （2）若函数在上有且仅有一个零点，

    ①求证：此零点是的极值点；

    ②求证：.

    （本题可能会用到的数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解观众对某综艺节目的评价情况，栏目组随机抽取了名观众进行评分调查(满分分)，并统计得到如图所示的频率分布直方图，以下说法错误的是（ ）

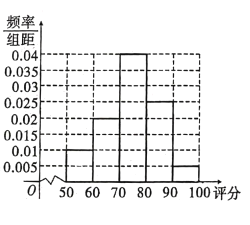
    A.参与评分的观众评分在的有人

    B.观众评分的众数约为分

    C.观众评分的平均分约为分

    D.观众评分的中位数约为分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，以椭圆E的长轴和短轴为对角线的四边形的面积为.

    （1）求椭圆E的方程；

    （2）若直线与椭圆E相交于A，B两点，设P为椭圆E上一动点，且满足（O为坐标原点）.当时，求的最小值.

    查看答案和解析>>

    同步练习册答案