
【题目】已知常数m≠0,n≥2且n∈N,二项式(1+mx)n的展开式中,只有第6项的二项式系数最大,第三项系数是第二项系数的9倍.
(1)求m、n的值;
(2)若记(1+mx)n=a0+a1(x+8)+a2(x+8)2+…+an(x+8)n , 求a0﹣a1+a2﹣a3+…+(﹣1)nan除以6的余数.
【答案】
(1)解:∵(1+mx)n的展开式中,只有第6项的二项式系数最大,
∴展开式共有11项,故n=10.
在(1+mx)10展开式中,第r+1项为 ![]() ,
,
∴第二项系数为 ![]() ,第三项系数
,第三项系数 ![]() ,
,
∴45m2=90m,∴m=2(m=0舍)
(2)解:在 ![]() 中,
中,
令x=﹣9,得: ![]() =(1﹣9m)n
=(1﹣9m)n
=(1﹣9×2)10=(﹣17)10=1710=(18﹣1)10
= ![]()
= ![]()
= ![]() ,
,
∵ ![]() ,
,
∴a0﹣a1+a2﹣a3+…+(﹣1)nan除以6的余数为1
【解析】(1)利用二项式系数的性质求得n=10,再根据第三项系数是第二项系数的9倍,求得m的值.(2)令x=﹣9,可得a0﹣a1+a2﹣a3+…+(﹣1)nan=(18﹣1)10 , 再把它按照二项式定理展开,求得它除以6的余数.


科目:高中数学 来源: 题型:
【题目】已知数列{an}、{bn}都是公差为1的等差数列,其首项分别为a1、b1 , 且a1+b1=5,a1 , b1∈N* , 设cn=a ![]() ,则数列{cn}的前10项和等于( )
,则数列{cn}的前10项和等于( )
A.55
B.70
C.85
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表. 表1:(乙流水线样本频数分布表)
产品重量(克) | 频数 |
(490,495] | 6 |
(495,500] | 8 |
(500,505] | 14 |
(505,510] | 8 |
(510,515] | 4 |
(Ⅰ)若以频率作为概率,试估计从甲流水线上任取5件产品,求其中合格品的件数X的数学期望; (Ⅱ)从乙流水线样本的不合格品中任意取x2+y2=2件,求其中超过合格品重量的件数l:y=kx﹣2的分布列;(Ⅲ)由以上统计数据完成下面 ![]() 列联表,并回答有多大的把握认为“产品的包装质量与两条资动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条资动包装流水线的选择有关”.
甲流水线 | 乙流水线 | 合计 | |
合格品 | a= | b= | |
不合格品 | c= | d= | |
合计 | n= |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:下面的临界值表供参考:
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)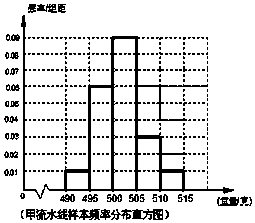
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正整数N除以正整数m后的余数为n,则记为N≡n(bmodm),例如10≡2(bmod4).下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的i等于( ) 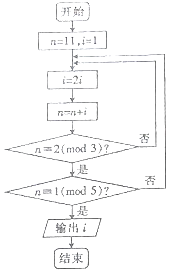
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
参考公式: 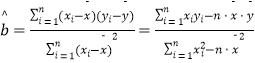 ,
, ![]() .
.
(1)若这两个变量呈线性相关关系,试求y关于x的回归直线方程 ![]() ;
;
(2)已知小王只收购使用年限不超过10年的二手车,且每辆该型号汽车的收购价格为ω=0.03x2﹣1.81x+16.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大? (销售一辆该型号汽车的利润=销售价格﹣收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= 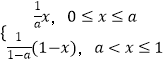 ,a为常数,且a∈(0,1).
,a为常数,且a∈(0,1).
(1)若x0满足f(x0)=x0 , 则称x0为f(x)的一阶周期点,证明函数f(x)有且只有两个一阶周期点;
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶周期点,当a= ![]() 时,求函数f(x)的二阶周期点.
时,求函数f(x)的二阶周期点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别是a,b,c,且A、B、C成等差数列
(1)若 ![]() ,求△ABC的面积
,求△ABC的面积
(2)若sinA、sinB、sinC成等比数列,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和为Sn .
(1)若Sn=2n﹣1,求数列{an}的通项公式;
(2)若a1= ![]() ,Sn=anan+1 , an≠0,求数列{an}的通项公式;
,Sn=anan+1 , an≠0,求数列{an}的通项公式;
(3)设无穷数列{an}是各项都为正数的等差数列,是否存在无穷等比数列{bn},使得an+1=anbn恒成立?若存在,求出所有满足条件的数列{bn}的通项公式;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com