已知f(x)=loga(a-ax)(a>0且a≠1).
(1)求f(x)的定义域;
(2)当a>1时,若不等式f-1(x2-mx+4)>f(x)在x∈[-3,-1]上恒成立,求实数m的取值范围.
解:(1)当0<a<1时,由a-a
x>0得x>1,此时定义域为(1,+∞);
当a>1时,由a-a
x>0得x<1,此时定义域为(-∞,1).
(2)令y=log
a(a-a
x),则a
y=a-a
x,解得x=log
a(a-a
y),
所以f
-1(x)=log
a(a-a
x)(a>0,x<1)
又因为函数y=log
a(a-a
x)(a>0,x<1)在定义域上单调递减,于是不等式f
-1(x
2-mx+4)>f(x)在x∈[-3,-1]上恒成立等价于不等式x
2-mx+4<x在x∈[-3,-1]上恒成立.
由于x∈[-3,-1],所以
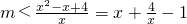
在x∈[-3,-1]上恒成立.
因函数
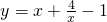
在区间[-3,-1]上的最小值为-6,所以m<-6.
分析:(1)由于是对数函数,故其真数大于0,再对a进行分类讨论;
(2)不等式f
-1(x
2-mx+4)>f(x)在x∈[-3,-1]上恒成立等价于不等式x
2-mx+4<x在x∈[-3,-1]上恒成立,从而分离参数
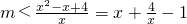
在x∈[-3,-1]上恒成立,从而可求实数m的取值范围.
点评:本题以对数函数为载体,考查函数的定义域,考查恒成立问题的处理,考查分离参数法,考查利用基本不等式求最值.

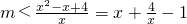 在x∈[-3,-1]上恒成立.
在x∈[-3,-1]上恒成立.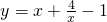 在区间[-3,-1]上的最小值为-6,所以m<-6.
在区间[-3,-1]上的最小值为-6,所以m<-6.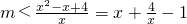 在x∈[-3,-1]上恒成立,从而可求实数m的取值范围.
在x∈[-3,-1]上恒成立,从而可求实数m的取值范围.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案