设函数f(x)=|x-1|,g(x)=|x-2|.
(Ⅰ)解不等式f(x)+g(x)<2;
(Ⅱ)对于实数x,y,若f(x)≤1,g(y)≤1,求证|x-2y+1|≤5.
解:(Ⅰ)不等式f(x)+g(x)<2,即|x-1|+|x-2|<2,
令 y=x-1|+|x-2|,则函数y=

,做出函数y的图象,
它与直线y=2的交点坐标为(

,2)和
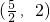
.
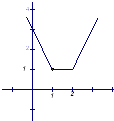
所以f(x)+g(x)<2的解集为

.----(5分)
(Ⅱ)因为 f(x)=|x-1|,g(y)=|y-2|,
而|x-2y+1|=|(x-1)-2(y-1)|≤|x-1|+2|y-1|=|x-1|+2|(y-2)+1|
≤|x-1|+2|(y-2)|+2=f(x)+2g(y)+2≤5.
所以|x-2y+1|≤5.--------(10分)
分析:(Ⅰ)不等式f(x)+g(x)<2,即|x-1|+|x-2|<2,令 y=x-1|+|x-2|,做出函数y的图象,它与直线y=2的交点坐标为(

,2)和
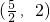
,由此求得f(x)+g(x)<2的解集.
(Ⅱ)利用绝对值不等式的性质可得|x-2y+1|=|(x-1)-2(y-1)|≤|x-1|+2|y-1|,同理可得|x-1|+2|y-1|
≤f(x)+2g(y)+2,结合条件得出结论.
点评:本题主要考查绝对值不等式的解法,分段函数的应用,体现了数形结合的数学思想,属于中档题.

 ,做出函数y的图象,
,做出函数y的图象, ,2)和
,2)和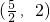 .
.
 .----(5分)
.----(5分) ,2)和
,2)和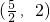 ,由此求得f(x)+g(x)<2的解集.
,由此求得f(x)+g(x)<2的解集.

 阅读快车系列答案
阅读快车系列答案