
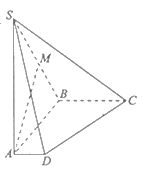
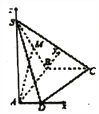
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
, ![]() 垂直于
垂直于![]() 和
和![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的二面角的余弦值;
所成的二面角的余弦值;
(Ⅲ)设点![]() 是直线
是直线![]() 上的动点,
上的动点, ![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】 试题分析:(1)以点![]() 为坐标原点,建立如图所示的空间直角坐标系,求得平面
为坐标原点,建立如图所示的空间直角坐标系,求得平面![]() 的一个法向量
的一个法向量![]() ,由
,由![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)易知平面![]() 的一个法向量为
的一个法向量为![]() ,设平面
,设平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,求得
,求得![]() ,即可求得平面
,即可求得平面![]() 与平面
与平面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
(3)设![]() ,则
,则![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,取得
,取得![]() 的表达式,利用二次函数的性质,即可求解
的表达式,利用二次函数的性质,即可求解![]() 的最大值.
的最大值.
试题解析:
(Ⅰ)以点![]() 为坐标原点,建立如图所示的空间直角坐标系,则
为坐标原点,建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则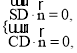 ∴
∴![]() 令
令![]() ,得
,得![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)易知平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,设平面
,设平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,
,
易知![]() ,则
,则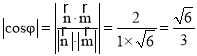 ,∴
,∴![]() ,
,
所以平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
(Ⅲ)设![]() ,则
,则![]() ,易知平面
,易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴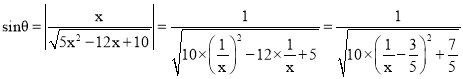 ,
,
当![]() ,即
,即![]() 时,
时, ![]() 取得最大值,且
取得最大值,且![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于
轴负半轴于![]() 点,且
点,且![]() 恰好是线段
恰好是线段![]() 的中点.
的中点.
(1)若过![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下, ![]() 是椭圆
是椭圆![]() 的左顶点,过点
的左顶点,过点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 的斜率分别为
的斜率分别为![]() ,试问:
,试问: ![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为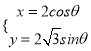 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,与直角坐标系
轴的正半轴为极轴,与直角坐标系![]() 取相同的单位长度建立极坐标系,曲线
取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)化曲线![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线![]() 与
与![]() 轴的一个交点的坐标为
轴的一个交点的坐标为![]() ,经过点
,经过点![]() 作斜率为1的直线,直线
作斜率为1的直线,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求线段
两点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.

(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:

现从该港口随机抽取了![]() 家公司,其中消防安全等级为三级的恰有20家.
家公司,其中消防安全等级为三级的恰有20家.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)按消防安全等级利用分层抽样的方法从这![]() 家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c已知ccosB+(b-2a)cosC=0
(1)求角C的大小
(2)若c=2,a+b=ab,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com