
分析 (1)由已知结合数量积公式求得$\overrightarrow{a}•\overrightarrow{b}$,然后求出$|2\overrightarrow{a}+\overrightarrow{b}{|}^{2}$得答案;
(2)由已知可得($\overrightarrow a+\overrightarrow b$)•($\overrightarrow a+k\overrightarrow b$)=0,展开后整理即可求得k值.
解答 解:(1)∵向量$\overrightarrow a$和$\overrightarrow b$的夹角为60°,且$|{\overrightarrow a}|=1,|{\overrightarrow b}|=2$,
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos60°=1×2×\frac{1}{2}=1$,
则$|2\overrightarrow{a}-\overrightarrow{b}{|}^{2}=4|\overrightarrow{a}{|}^{2}-4\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}=4-4×1+4=4$,
∴$|{\overrightarrow{2a}-\overrightarrow b}|$=2;
(2)∵向量$\overrightarrow a+\overrightarrow b$和向量$\overrightarrow a+k\overrightarrow b$垂直,
∴($\overrightarrow a+\overrightarrow b$)•($\overrightarrow a+k\overrightarrow b$)=$|\overrightarrow{a}{|}^{2}+(k+1)\overrightarrow{a}•\overrightarrow{b}+k|\overrightarrow{b}{|}^{2}=1+(k+1)+4k=0$,
解得:k=$-\frac{2}{5}$.
点评 本题考查平面向量的数量积运算,考查了向量垂直与数量积间的关系,是中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
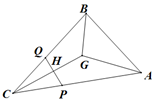 如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )
如图,在△ABC中,$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,$\overrightarrow{CA}$=$\overrightarrow{a}$,$\overrightarrow{CB}$=$\overrightarrow{b}$,已知点P,Q分别为线段CA,CB(不含端点)上的动点,PQ与CG交于H,且H为线段CG中点,若$\overrightarrow{CP}$=m$\overrightarrow{a}$,$\overrightarrow{CQ}$=n$\overrightarrow{b}$,则$\frac{1}{m}$+$\frac{1}{n}$=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com