
【题目】【扬州市2016—2017学年度第一学期期末检测】(本小题满分14分)
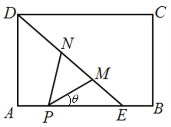
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
【答案】见解析
【解析】⑴方法一:在![]() PME中,
PME中,![]() ,PE=AE-AP=4米,
,PE=AE-AP=4米,![]() ,
,![]() ,
,
由正弦定理得![]() ,
,
所以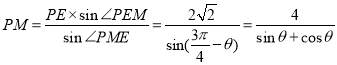 ,---------------------2分
,---------------------2分
同理在![]() PNE中,由正弦定理得
PNE中,由正弦定理得![]() ,
,
所以 ,---------------------4分
,---------------------4分
所以![]() PMN的面积S
PMN的面积S![]()
![]()
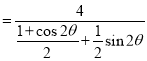
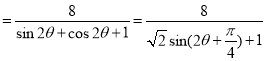 ,--------------------8分
,--------------------8分
当M与E重合时,![]() ;当N与D重合时,
;当N与D重合时,![]() ,即
,即![]() ,
,![]() ,
,
所以![]() .
.
综上可得: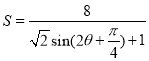 ,
,![]() .---------------------10分
.---------------------10分
方法二:在![]() PME中,
PME中,![]() ,PE=AE-AP=4米,
,PE=AE-AP=4米,![]() ,
,![]() ,由正弦定理可知:
,由正弦定理可知:![]() ,
,
所以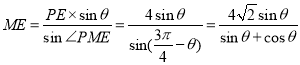 ,---------------------2分
,---------------------2分
在![]() PNE中,由正弦定理可知:
PNE中,由正弦定理可知:![]() ,
,
所以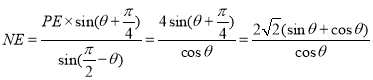 ,---------------------4分
,---------------------4分
所以![]() ,
,
又点P到DE的距离为![]() ,---------------------6分
,---------------------6分
所以![]() PMN的面积S=
PMN的面积S=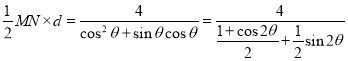
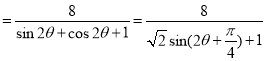 ,---------------------8分
,---------------------8分
当M与E重合时,![]() ;当N与D重合时,
;当N与D重合时,![]() ,即
,即![]() ,
,![]() ,
,
所以![]() .
.
综上可得: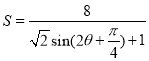 ,
,![]() .---------------------10分
.---------------------10分
⑵当![]() 即
即![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .---------13分
.---------13分
所以可视区域![]() PMN面积的最小值为
PMN面积的最小值为![]() 平方米.---------------------14分
平方米.---------------------14分


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】【2017南通一模19】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() ,证明:函数
,证明:函数![]() 有且只有一个零点;
有且只有一个零点;
(3)若函数![]() 又两个零点,求实数
又两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为 ![]() +
+ ![]() ;
;
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497﹣﹣512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(1)求证:DA1⊥ED1;
(2)若直线DA1与平面CED1成角为45°,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福州市某大型家电商场为了使每月销售空调和冰箱获得的总利润达到最大,对某月即将出售的空调和冰箱进行了相关调查,得出下表:
资金 | 每台空调或冰箱所需资金(百元) | 月资金最多供应量(百元) | |
空调 | 冰箱 | ||
进货成本 | 30 | 20 | 300 |
工人工资 | 5 | 10 | 110 |
每台利润 | 6 | 8 | |
问:该商场如果根据调查得来的数据,应该怎样确定空调和冰箱的月供应量,才能使商场获得的总利润最大?总利润的最大值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣1|+x2+kx.
(1)若对于区间(0,+∞)内的任意x,总有f(x)≥0成立,求实数k的取值范围;
(2)若函数f(x)在区间(0,2)内有两个不同的零点x1 , x2 , 求:
①实数k的取值范围;
② ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B为曲线C:y=![]() 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM![]() BM,求直线AB的方程.
BM,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com