
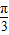 ),sin(α+
),sin(α+ )),点C(1,0).
)),点C(1,0).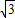 ,求α的值;
,求α的值;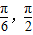 ),求
),求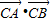 的取值范围.
的取值范围.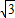 ,可得 (cosα-1)2+sin2α=3,化简可得cosα=-
,可得 (cosα-1)2+sin2α=3,化简可得cosα=- ,由此求得 α 的值.
,由此求得 α 的值.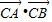 的解析式为
的解析式为  +
+ sin(α-
sin(α-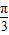 ),由α∈(
),由α∈(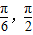 ),可得 α-
),可得 α-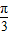 ∈[-
∈[-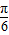 ,
,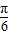 ],再根据正弦函数的定义域和值域求得
],再根据正弦函数的定义域和值域求得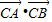 的取值范围.
的取值范围.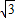 ,则有 (cosα-1)2+sin2α=3,化简可得cosα=-
,则有 (cosα-1)2+sin2α=3,化简可得cosα=- ,∴α=2kπ+
,∴α=2kπ+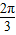 ,或α=2kπ+
,或α=2kπ+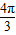 ,k∈z.
,k∈z.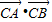 =(cosα-1,sinα)•(cos(α+
=(cosα-1,sinα)•(cos(α+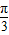 )-1,sin(α+
)-1,sin(α+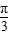 ))=(cosα-1)[cos(α+
))=(cosα-1)[cos(α+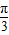 )-1]+sinα•sin(α+
)-1]+sinα•sin(α+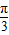 )
) cosα-
cosα-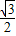 sinα-1)+sinα(
sinα-1)+sinα( sinα+
sinα+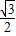 cosα)=
cosα)= cos2α-
cos2α-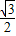 sinαcosα-cosα-
sinαcosα-cosα-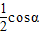 +
+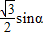 +1+
+1+ sin2α+
sin2α+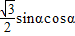
 -
- cosα+
cosα+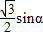 =
= +
+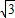 (
( sinα-
sinα-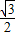 cosα)=
cosα)= +
+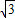 sin(α-
sin(α-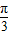 ),
),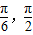 ),可得 α-
),可得 α-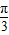 ∈[-
∈[-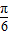 ,
,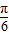 ],∴-
],∴- ≤sin(α-
≤sin(α-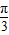 )≤
)≤ ,∴-
,∴-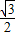 ≤
≤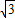 sin(α-
sin(α-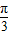 )≤
)≤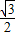 ,
,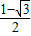 ≤
≤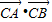 ≤
≤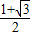 ,即
,即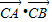 的取值范围是[
的取值范围是[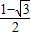 ,
,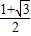 ].
].

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| CA |
| CB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| AB |
| OB |
| AB |
| OB |
查看答案和解析>>
科目:高中数学 来源:闵行区二模 题型:解答题
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| AB |
| OB |
| AB |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com