证明:(I)∵对于任意实数m,n,恒有f(m+n)=f(m)•f(n)
令m=1,(1)=f(1)f(0)
∵x>0时,0<f(x)<1
∴0<f(1)<1
∴f(0)=1
(II)当x<0时,-x>0,则0<f(-x)<1
∵f(0)=f(x)f(-x)=1
∴

∴f(x)>1
(Ⅲ)设x
1<x
2则x
1-x
2<0
由II可得f(x
1-x
2)>1
∵f(x
1)=f[(x
1-x
2)+x
2]=f(x
1-x
2)+f(x
2)>f(x
2)
∴函数f(x)单调递减
(IV)∵f(3)=f(1)f(2)=f
3(1)=

∴
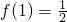
∵f(m+n)=f(m)•f(n)对任意的m,n都成立
f(2002)=f
2002(1)=

分析:(I)由f(m+n)=f(m)•f(n),令m=1,(1)=f(1)f(0)及x>0时,0<f(x)<1可求f(0)
(II)当x<0时,-x>0,则0<f(-x)<1,而f(0)=f(x)f(-x)=1可得

,从而可得f(x)与1的大小
(III)设x
1<x
2则x
1-x
2<0,由II可得f(x
1-x
2)>1,而f(x
1)=f[(x
1-x
2)+x
2]=f(x
1-x
2)+f(x
2)可判断函数的单调性
(IV)由f(3)=f(1)f(2)=f
3(1)=

可求f(1),进而可求f(2002)
点评:本题主要考查了抽象函数的函数值的求解,主要采用的赋值法,构造x
1=x
1-x
2+x
2,是证明函数的单调性的 关键,属于函数知识的综合应用.

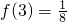 ,试求f(2002)的值.
,试求f(2002)的值.

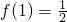

 ,从而可得f(x)与1的大小
,从而可得f(x)与1的大小 可求f(1),进而可求f(2002)
可求f(1),进而可求f(2002)
