练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】从岳阳到郴州的快速列车包括起始站和终点站共有六站，将这六站分别记为.有一天，张兵和其他18 名旅客乘同一车厢离开岳阳，这些旅客中有些是湖北人，其他的是湖南人，认识所有同车厢旅客的张兵观测到:除了终点站，在每一站，当火车到达时，这节车厢上的湖南人的数目与下车旅客的数目相同，且这次行程中没有新的旅客进入这节车厢.张兵又进一步观测到:当火车离开站时，车厢内有 12名旅客；当火车离开站时，还有 7 名旅客在这一车厢内；当他准备在站下车时，还有5名旅客在这一车厢内.试问开始时火车的这一节车厢有多少湖北人，有多少湖南人？且在旅途中这些数目如何变化？

    【答案】见解析

    【解析】

    由条件得在站有7人下车，即19名旅客中有7个湖南人，在站有2人下车，即在途中有2个湖南人，中至少有2个湖南人，在站至少有2人下车，所以，站后车厢至少有9人.又因为，所以，途中至少有3个湖南人，因此，经过站后车厢内至多有9人，故经过站后车厢内有9人.

    综上所述，段有7个湖南人，12个湖北人；站有4个湖南人、3个湖北人下车，站有1个湖南人、2个湖北人下车，站有2个湖北人下车，站有2个人下车.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】甲、乙两位同学参加诗词大赛，各答3道题，每人答对每道题的概率均为，且各人是否答对每道题互不影响.

    （Ⅰ）用表示甲同学答对题目的个数，求随机变量的分布列和数学期望；

    （Ⅱ）设为事件“甲比乙答对题目数恰好多2”，求事件发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知公差不为零的等差数列{an）满足a1＝5，且a3，a6，a11成等比数列．

    （1）求数列{an}的通项公式；

    （2）设bn＝an·3n－1，求数列{bn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某隧道的剖面图是由半圆及矩形组成，交通部门拟在隧道顶部安装通风设备（视作点），为了固定该设备，计划除从隧道最高点处使用钢管垂直向下吊装以外，再在两侧自两点分别使用钢管支撑.已知道路宽，设备要求安装在半圆内部，所使用的钢管总长度为.

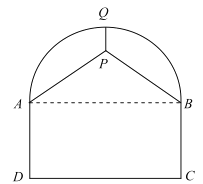
    （1）①设，将表示为关于的函数；

    ②设，将表示为关于的函数；

    （2）请选用（1）中的一个函数关系式，说明如何设计，所用的钢管材料最省？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位选派甲乙丙三人组队参加知识竞赛，甲乙丙三人在同时回答一道问题时，已知甲答对的概率是，甲丙两人都答错的概率是，乙丙两人都答对的概率是，规定每队只要有一人答对此题则该队答对此题．

    （1）求该单位代表队答对此题的概率；

    （2）此次竞赛规定每队都要回答10道必答题，每道题答对得20分，答错得分．若该单位代表队答对每道题的概率相等且回答任一道题的对错对回答其他题没有影响，求该单位代表队必答题得分的均值(精确到1分)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．

    （1）求图中的值；

    （2）根据频率分布直方图，估计这100名学生语文成绩的平均分，众数，中位数；

    （3）若这100名学生语文成绩某些分数段的人数（）与数学成绩相应分数段的人数（）之比如下表所示，求数学成绩在[50，90）之外的人数．

    分数段

    [50，60）

    [60，70）

    [70，80）

    [80，90）

    1：1

    2：1

    3：4

    4：5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市为创建全国文明城市，推出“行人闯红灯系统建设项目”，将针对闯红灯行为进行曝光.交警部门根据某十字路口以往的监测数据，从穿越该路口的行人中随机抽查了人，得到如图示的列联表：

    闯红灯

    不闯红灯

    合计

    年龄不超过岁

    年龄超过岁

    合计

    （1）能否有的把握认为闯红灯行为与年龄有关？

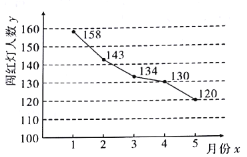
    （2）下图是某路口监控设备抓拍的个月内市民闯红灯人数的统计图.请建立与的回归方程，并估计该路口月份闯红灯人数.

    附：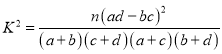

    ，

    参考数据：，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在的客户称为“熟客”,并把他们去年采购的数量制成下表:

    采购数x

    客户数

    10

    10

    5

    20

    5

    (1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;

    (2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);

    (3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元()销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《普通高中数学课程标准（版）》提出了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平，现以六大素养为指标对二人进行了测验，根据测验结果绘制了雷达图（如图，每项指标值满分为分，分值高者为优，低者为差），则下面叙述不正确的是（ ）

    A.甲的数据分析素养低于乙

    B.乙的六大素养中逻辑推理最差

    C.甲的数学建模素养差于逻辑推理素养

    D.乙的六大素养整体平均水平优于甲

    查看答案和解析>>

    同步练习册答案