练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】由于浓酸泄漏对河流形成了污染，现决定向河中投入固体碱，1个单位的固体碱在水中逐步溶化，水中的碱浓度与时间的关系，可近似地表示为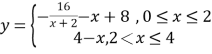，只有当河流中碱的浓度不低于1时，才能对污染产生有效的抑制作用.

    （1）如果只投放1个单位的固体碱，则能够维持有效抑制作用的时间有多长？

    （2）当河中的碱浓度开始下降时，即刻第二次投放1个单位的固体碱，此后，每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和，求河中碱浓度可能取得的最大值.

    【答案】（1）；（2）.

    【解析】

    （1）,

    ,

    综上，得.

    即若1个单位的固体碱只投放一次，则能够维持有效抑制作用的时间为.

    （2）当时，单调递增,

    当时，y=4-x单调递减,

    所以当河中的碱浓度开始下降时，即刻第二次投放1个单位的固体碱，

    即时，,

    故当且仅当时，y有最大值.

    本试题主要考查了函数在实际生活中的运用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4—5：不等式选讲

    设．

    （1）当时，解不等式；

    （2）若对任意恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在上的函数满足任意都有，且时，，则，，的大小关系是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义域为的函数满足，当时，.若时，恒成立，则实数的取值范围是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）求函数的极值点；

    （2）设函数有两个零点，求整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥的两条棱长为1，其余四条棱长为2，有下列命题：

    该三棱锥的体积是；

    该三棱锥内切球的半径是；

    该三棱锥外接球的表面积是．

    其中正确的是　　

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正六棱锥中，已知底边为2，侧棱与底面所成角为.

    （1）求该六棱锥的体积；

    （2）求证：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在①；②，这两个条件中任选一个，补充在下面问题中，然后解答补充完整的题目.

    在中，内角的对边分别为，设的面积为，已知 .

    （1）求的值；

    （2）若，求的值.

    注：如果选择多个条件分别解答，按第一个解答计分.

    查看答案和解析>>

    同步练习册答案