
【题目】随着人民生活水平的日益提高,某小区居民拥有私家车的数量与日俱增.由于该小区建成时间较早,没有配套建造地下停车场,小区内无序停放的车辆造成了交通的拥堵.该小区的物业公司统计了近五年小区登记在册的私家车数量(累计值,如147表示2016年小区登记在册的所有车辆数,其余意义相同),得到如下数据:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
数量 | 37 | 104 | 147 | 196 | 216 |
(1)若私家车的数量![]() 与年份编号
与年份编号![]() 满足线性相关关系,求
满足线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2020年该小区的私家车数量;
的线性回归方程,并预测2020年该小区的私家车数量;
(2)小区于2018年底完成了基础设施改造,划设了120个停车位.为解决小区车辆乱停乱放的问题,加强小区管理,物业公司决定禁止无车位的车辆进入小区.由于车位有限,物业公司决定在2019年度采用网络竞拍的方式将车位对业主出租,租期一年,竞拍方案如下:①截至2018年己登记在册的私家车业主拥有竞拍资格;②每车至多中请一个车位,由车主在竞拍网站上提出申请并给出自己的报价;③根据物价部门的规定,竞价不得超过1200元;④申请阶段截止后,将所有申请的业主报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则以提出申请的时间在前的业主成交,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的40位业主,进行了竞拍意向的调查,并对他们的拟报竞价进行了统计,得到如图频率分布直方图:

(i)求所抽取的业主中有意向竞拍报价不低于1000元的人数;
(ii)如果所有符合条件的车主均参与竞拍,利用样本估计总体的思想,请你据此预测至少需要报价多少元才能竞拍车位成功?(精确到整数)
参考公式及数据:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: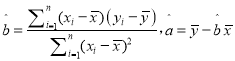 ;
;.
【答案】(1)![]() ,320;(2)(i)12人;(ii)936.
,320;(2)(i)12人;(ii)936.
【解析】
(1)由表中数据,计算得![]() 与
与![]() 的值,则线性回归方程可求,取x=7求得y值得答案;
的值,则线性回归方程可求,取x=7求得y值得答案;
(2)(i)由频率直方图求得有意竞拍报价不低于1000元的频率,乘以40得答案.
(ii)由题意,![]() .由频率直方图估算知,报价应该在900-1000之间,设报价为x百元,可得
.由频率直方图估算知,报价应该在900-1000之间,设报价为x百元,可得![]() .求解x值即可.
.求解x值即可.
(1)由表中数据,计算得![]() ,
,![]() ,
, ,
,![]() .
.
故所求线性回归方程为![]() ,
,
令x=7,得![]() ;
;
(2)(i)由频率直方图可知,有意竞拍报价不低于1000元的频率为:
(0.25+0.05)×1=0.3,
共抽取40位业主,则40×0.3=12,
∴有意竞拍不低于1000元的人数为12人.
(ii)由题意,![]() .
.
由频率直方图估算知,报价应该在900-1000之间,
设报价为x百元,
则![]() .
.
解得x≈9.36.
∴至少需要报价936元才能竞拍成功.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方为
的参数方为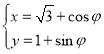 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求直线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)设![]() ,
,![]() ,
,![]() 为直线
为直线![]() 与曲线
与曲线![]() 的两个交点,求
的两个交点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,离心率
的左、右焦点,离心率![]() ,过椭圆
,过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(Ⅲ)设点![]() 是一个动点,若直线
是一个动点,若直线![]() 的斜率存在,且
的斜率存在,且![]() 为
为![]() 中点,
中点,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为F,过点F的直线交抛物线于A,B两点.
的焦点为F,过点F的直线交抛物线于A,B两点.
(1)若![]() ,求直线AB的斜率;
,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某商场随机抽取了2000件商品,按商品价格(元)进行统计,所得频率分布直方图如图所示.记价格在![]() ,
,![]() ,
,![]() 对应的小矩形的面积分别为
对应的小矩形的面积分别为![]() ,且
,且![]() .
.
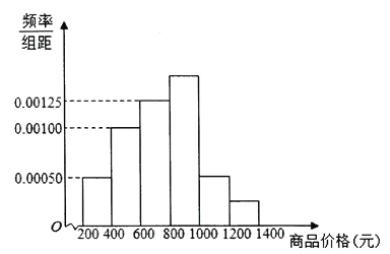
(1)按分层抽样从价格在![]() ,
,![]() 的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
(2)在清明节期间,该商场制定了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表,如果你是消费者,你会选择哪种方案?为什么?(同一组中的数据用该组区间中点值作代表)
商品价格 |
|
|
|
|
|
|
优惠(元) | 30 | 50 | 140 | 160 | 280 | 320 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com