
【题目】如图,已知点![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,连接
的中点,连接![]() .现将
.现将![]() 沿
沿![]() 折叠至Δ
折叠至Δ![]() 的位置,连接
的位置,连接![]() .记平面
.记平面 ![]() 与平面
与平面 ![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.


(1)证明: ![]()
(2)证明: ![]()
(3)求平面![]() 与平面
与平面 ![]() 所成锐二面角大小.
所成锐二面角大小.
【答案】(1)见解析;(2)见解析;(3)![]()
![]() .
.
【解析】试题分析:(1)由![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,根据三角形中位线定理可得
的中点,根据三角形中位线定理可得![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,再利用线面平行的性质定理可得结论;(2)由三角形中位线定理以可判定四边形
,再利用线面平行的性质定理可得结论;(2)由三角形中位线定理以可判定四边形![]() 平行四边形,进而可得四边形
平行四边形,进而可得四边形![]() 为菱形,于是可得
为菱形,于是可得![]() ,
, ![]() ,
,![]()
![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,从而根据面面垂直的判定定理可得结论;(3)作
,从而根据面面垂直的判定定理可得结论;(3)作![]() 于
于![]() 交
交![]() 于
于![]() ,可知
,可知![]() 是
是![]() 的中点,折叠后角
的中点,折叠后角![]() 是二面角
是二面角![]() 的平面角,可证明等腰
的平面角,可证明等腰![]() 的底角
的底角![]() 是平面
是平面![]() 与平面
与平面![]() 所成锐二面角的平面角,进而可得结果.
所成锐二面角的平面角,进而可得结果.
试题解析:(1)证明:因为![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,所以
的中点,所以![]() 经过
经过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
, ![]()
![]()
又![]()
![]() ,
,![]()
![]() .
.
(2)证明:记![]()
![]()
![]() 且
且![]()
![]()
![]() ,
,![]() 四边形
四边形![]()
又![]()
![]() ,
,![]()
![]() .
.
![]()
![]() ,
,![]()
![]() 则得
则得![]() .
.
又![]() ,
,![]()
![]() .
.
(3) 过![]() ,易知
,易知![]() 是
是![]() 的中点,
的中点,
易知折叠后角![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]()
![]() ,
,
则可知![]() .
.
![]()
![]() .易知
.易知![]()
![]() 等腰
等腰![]() 的底角角
的底角角![]() 是
是![]() 所成锐二面角的平面角,
所成锐二面角的平面角,
易知角![]()
![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的判定定理、二面角的求法,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|![]() |;
|;
(2)已知点D是AB上一点,满足![]() =λ
=λ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足![]() =λ
=λ![]() .
.
①当λ=![]() 时,求
时,求![]()
![]() ;
;
②是否存在非零实数λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ ![]() x2(a∈R).
x2(a∈R).
(1)若x>0,恒有f(x)≤x成立,求实数a的取值范围;
(2)若a=0,求f(x)在区间[t,t+2](t>0)上的最小值;
(3)若函数g(x)=f(x)﹣x有两个极值点x1 , x2 , 求证: ![]() +
+ ![]() >2ae.
>2ae.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)在R上的导函数为f'(x),对于任意的实数x,都有f'(x)+2017<4034x,若f(t+1)<f(﹣t)+4034t+2017,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人的各科成绩如图中的茎叶图所示,则下列说法不正确的是( )
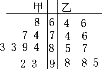
A. 甲、乙两人的各科平均分相同
B. 甲各科成绩的中位数是83,乙各科成绩的中位数是85
C. 甲各科成绩比乙各科成绩稳定
D. 甲各科成绩的众数是89,乙各科成绩的众数为87
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com