
【题目】如图是一几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() 分别为
分别为![]() 的中点.在此几何体中,给出下列结论,其中正确的结论是( )
的中点.在此几何体中,给出下列结论,其中正确的结论是( )

A.平面![]() 平面
平面![]() B.直线
B.直线![]() 平面
平面![]()
C.直线![]() 平面
平面![]() D.直线
D.直线![]() 平面
平面![]()
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】某地区为了解群众上下班共享单车使用情况,根据年龄按分层抽样的方式调查了该地区50名群众,他们的年龄频数及使用共享单车人数分布如下表:
年龄段 | 20~29 | 30~39 | 40~49 | 50~60 |
频数 | 12 | 18 | 15 | 5 |
经常使用共享单车 | 6 | 12 | 5 | 1 |
(1)由以上统计数据完成下面的![]() 列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | |||
不经常使用共享单车 | |||
总计 |
附: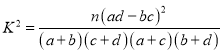 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(2)若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人,再从这6人中随机抽取2人,求这2人中恰好有1人年龄在30~39岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 、
、![]() 、
、![]() 为平面直角坐标系中两两不同的点。若
为平面直角坐标系中两两不同的点。若![]() ,
,![]() ,且
,且![]() ,则称点
,则称点![]() 、
、![]() 调和分割点
调和分割点![]() 、
、![]() 。已知平面上点
。已知平面上点![]() 、
、![]() 调和分割点
调和分割点![]() 、
、![]() .则下面说法正确的是()。
.则下面说法正确的是()。
A. ![]() 可能是线段
可能是线段![]() 的中点
的中点
B. ![]() 可能是线段
可能是线段![]() 的中点
的中点
C. 点![]() 、
、![]() 可能同时在线段
可能同时在线段![]() 上
上
D. 点![]() 、
、![]() 不可能同时在线段
不可能同时在线段![]() 的延长线上
的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为![]() 记
记![]() .
.
(1)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
,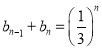 .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com