
【题目】设点Pi(xi , yi)在直线li:aix+biy=ci上,若ai+bi=ici(i=1,2),且|P1P2|≥ ![]() 恒成立,则
恒成立,则 ![]() +
+ ![]() = .
= .
科目:高中数学 来源: 题型:
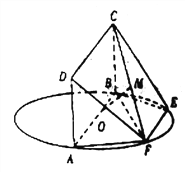
【题目】如图所示, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)设![]() 的中点为
的中点为![]() ,求三棱锥
,求三棱锥![]() 的体积
的体积![]() 与多面体
与多面体![]() 的体积
的体积![]() 之比的值.
之比的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料![]() ,五合板
,五合板![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料![]() 、五合板
、五合板![]() ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓![]() 、五合板
、五合板![]() .出售一张书桌可获利润
.出售一张书桌可获利润![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润![]() 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点. 
(1)求证:平面PAB∥平面EFG;
(2)证明:平面EFG⊥平面PAD;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ),在以坐标原点为极点,
),在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(1)试将曲线![]() 与
与![]() 化为直角坐标系
化为直角坐标系![]() 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时![]() 的取值范围;
的取值范围;
(2)当![]() 时,两曲线相交于
时,两曲线相交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 A(x1 , y1),B(x2 , y2)是函数f(x)=x﹣ ![]() 的图象上任意两点,若 M为 A,B的中点,且 M的横坐标为1.
的图象上任意两点,若 M为 A,B的中点,且 M的横坐标为1.
(1)求y1+y2;
(2)若Tn= ![]() ,n∈N* , 求 Tn;
,n∈N* , 求 Tn;
(3)已知数列{an}的通项公式an= ![]() (n≥1,n∈N*),数列{an}的前n项和为Sn , 若不等式2nSn<m2n﹣4Tn+5对任意n∈N*恒成立,求m的取值范围.
(n≥1,n∈N*),数列{an}的前n项和为Sn , 若不等式2nSn<m2n﹣4Tn+5对任意n∈N*恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com